Article contents
Pattern evolution and modal decomposition of Faraday waves in a brimful cylinder
Published online by Cambridge University Press: 10 November 2023
Abstract
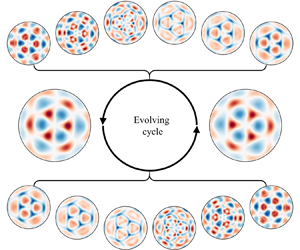
This paper investigates the steady-state pattern evolution of symmetric Faraday waves excited in a brimful cylindrical container when driving parameters much exceed critical thresholds. In such liquid systems, parametric surface responses are typically considered as the resonant superposition of unstable standing waves. A modified free-surface synthetic Schlieren method is employed to obtain full three-dimensional spatial reconstructions of instantaneous surface patterns. Multi-azimuth structures and localized travelling waves during the small-elevation phases of the oscillation cycle give rise to modal decomposition in the form of  $\nu$-basis modes. Two-step surface-fitting results provide insight into the spatiotemporal characteristics of dominant wave components and corresponding harmonics in the experimental observations. Arithmetic combination of modal indices and uniform frequency distributions reveal the nonlinear mechanisms behind pattern formation and the primary pathways of energy transfer. Taking the hypothetical surface manifestation of multiple azimuths as the modal solutions, a linear stability analysis of the inviscid system is utilised to calculate fundamental resonance tongues (FRTs) with non-overlapping bottoms, which correspond to subharmonic or harmonic
$\nu$-basis modes. Two-step surface-fitting results provide insight into the spatiotemporal characteristics of dominant wave components and corresponding harmonics in the experimental observations. Arithmetic combination of modal indices and uniform frequency distributions reveal the nonlinear mechanisms behind pattern formation and the primary pathways of energy transfer. Taking the hypothetical surface manifestation of multiple azimuths as the modal solutions, a linear stability analysis of the inviscid system is utilised to calculate fundamental resonance tongues (FRTs) with non-overlapping bottoms, which correspond to subharmonic or harmonic  $\nu$-basis modes induced by surface instability at the air–liquid interface. Close relationships between experimental observations and corresponding FRTs provide qualitative verification of dominant modes identified using surface-fitting results. This supports the validity and rationality of the applied
$\nu$-basis modes induced by surface instability at the air–liquid interface. Close relationships between experimental observations and corresponding FRTs provide qualitative verification of dominant modes identified using surface-fitting results. This supports the validity and rationality of the applied  $\nu$-basis modes.
$\nu$-basis modes.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 4
- Cited by


