Published online by Cambridge University Press: 06 October 2020
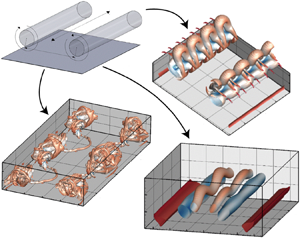
The transient growth of a counter-rotating equal strength vortex pair, which descends under mutual induction towards a ground plane, is examined through non-modal linear stability analysis and direct numerical simulation. The vortex pair is studied at a height of five vortex spacing distances above the wall, consistent with the first mode of vortex instability/wall interaction observed by experiment. Three regimes are identified in which the optimal mode topology and non-modal growth mechanisms are distinct, correlated with the widely studied Crow and elliptic instabilities, alongside a wall-modified long-wavelength-displacement-type instability. The initial optimal amplification mechanisms are found to be weakly influenced by the wall, with the long- and short-wave mechanisms consisting of anti-symmetric amplification at the leading hyperbolic point and symmetric amplification at the trailing hyperbolic point, respectively, as observed by out-of-wall studies previously. The linear growth of the Crow instability is found to be impeded by the wall, and the evolution results in the suppression of both the secondary structure formation and vortex rebound. The linear elliptic mode remains largely uninhibited however, and substantially outgrows the long-wave modes, illustrating the importance of the elliptic instability on the wall-bounded interaction. Both the wall-modified long-wave and elliptic optimal growth modes show substantial amplification in the secondary vortices. At finite perturbation amplitudes, the nonlinear formation of both long- and short-wavelength secondary vortex tongues are shown to play a critical role in the vortex dynamics as the pair strongly interacts with the wall.