Article contents
Optimal eddy viscosity for resolvent-based models of coherent structures in turbulent jets
Published online by Cambridge University Press: 28 April 2021
Abstract
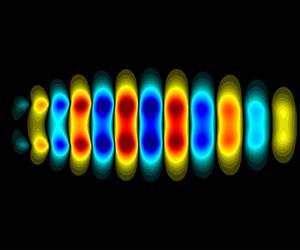
Response modes computed via linear resolvent analysis of a turbulent mean-flow field have been shown to qualitatively capture characteristics of the observed turbulent coherent structures in both wall-bounded and free shear flows. To make such resolvent models predictive, the nonlinear forcing term must be closed. Strategies to do so include imposing self-consistent sets of triadic interactions, proposing various source models or through turbulence modelling. For the latter, several investigators have proposed using the mean-field eddy viscosity acting linearly on the fluctuation field. In this study, a data-driven approach is taken to quantitatively improve linear resolvent models by deducing an optimal eddy-viscosity field that maximizes the projection of the dominant resolvent mode to the energy-optimal coherent structure educed using spectral proper orthogonal decomposition (SPOD) of data from high-fidelity simulations. We use large-eddy simulation databases for round isothermal jets at subsonic, transonic and supersonic conditions and show that the optimal eddy viscosity substantially improves the agreement between resolvent and SPOD modes, reaching over 90 % agreement at those frequencies where the jet exhibits a low-rank response. We then consider a fixed model for the eddy viscosity and show that with the calibration of a single constant, the results are generally close to the optimal one. In particular, the use of a standard Reynolds-averaged Navier–Stokes eddy-viscosity resolvent model, with a single coefficient, provides substantial agreement between SPOD and resolvent modes for three turbulent jets and across the most energetic wavenumbers and frequencies.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 85
- Cited by


