Article contents
Open-loop control of cavity oscillations with harmonic forcings
Published online by Cambridge University Press: 12 September 2012
Abstract
This article deals with open-loop control of open-cavity flows with harmonic forcings. Two-dimensional laminar open-cavity flows usually undergo a supercritical Hopf bifurcation at some critical Reynolds number: a global mode becomes unstable and its amplitude converges towards a limit cycle. Such behaviour may be accurately captured by a Stuart–Landau equation, which governs the amplitude of the global mode. In the present article, we study the effect on such a flow of a forcing characterized by its frequency 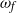 , its amplitude
, its amplitude 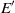 and its spatial structure
and its spatial structure 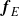 . The system reacts like a forced Van der Pol oscillator. In the general case, such a forcing modifies the linear dynamics of the global mode. It is then possible to predict preferred forcing frequencies
. The system reacts like a forced Van der Pol oscillator. In the general case, such a forcing modifies the linear dynamics of the global mode. It is then possible to predict preferred forcing frequencies 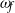 , at which the global mode may be stabilized with the smallest possible forcing amplitude
, at which the global mode may be stabilized with the smallest possible forcing amplitude 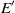 . In the case of a forcing frequency close to the frequency of the global mode, a locking phenomenon may be observed if the forcing amplitude
. In the case of a forcing frequency close to the frequency of the global mode, a locking phenomenon may be observed if the forcing amplitude 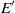 is sufficiently high: the frequency of the flow on the limit cycle may be modified with a very small forcing amplitude
is sufficiently high: the frequency of the flow on the limit cycle may be modified with a very small forcing amplitude 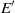 . In each case, we compute all harmonics of the flow field and all coefficients that enter the amplitude equations. In particular, it is possible to find preferred forcing structures
. In each case, we compute all harmonics of the flow field and all coefficients that enter the amplitude equations. In particular, it is possible to find preferred forcing structures 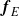 that achieve strongest impact on the flow field. In the general case, these are the optimal forcings, which are defined as the forcings that trigger the strongest energy response. In the case of a forcing frequency close to the frequency of the global mode, a forcing structure equal to the adjoint global mode ensures the lowest forcing amplitude
that achieve strongest impact on the flow field. In the general case, these are the optimal forcings, which are defined as the forcings that trigger the strongest energy response. In the case of a forcing frequency close to the frequency of the global mode, a forcing structure equal to the adjoint global mode ensures the lowest forcing amplitude 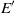 . All predictions given by the amplitude equations are checked against direct numerical simulations conducted at a supercritical Reynolds number. We show that a global mode may effectively be stabilized by a high-frequency harmonic forcing, which achieves suppression of the perturbation frequencies that are lower than the forcing frequency, and that a near-resonant forcing achieves locking of the flow onto the forcing frequency, as predicted by the amplitude equations.
. All predictions given by the amplitude equations are checked against direct numerical simulations conducted at a supercritical Reynolds number. We show that a global mode may effectively be stabilized by a high-frequency harmonic forcing, which achieves suppression of the perturbation frequencies that are lower than the forcing frequency, and that a near-resonant forcing achieves locking of the flow onto the forcing frequency, as predicted by the amplitude equations.
Information
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
- 36
- Cited by

