Article contents
Open capillary siphons
Published online by Cambridge University Press: 09 December 2021
Abstract
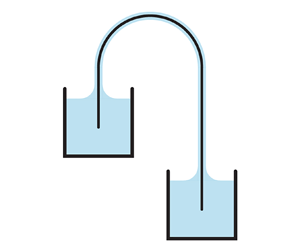
Flow in the inverted U-shaped tube of a conventional siphon can be established and maintained only if the tube is filled and closed, so that air does not enter. We report on siphons that operate entirely open to the atmosphere by exploiting surface tension effects. Such capillary siphoning is demonstrated by paper tissue that bridges two containers and conveys water from the upper to the lower. We introduce a more controlled system consisting of grooves in a wetting solid, formed here by pressing together hook-shaped metallic rods. The dependence of flux on siphon geometry is systematically measured, revealing behaviour different from the conventional siphon. The flux saturates when the height difference between the two container's free surfaces is large; it also has a strong dependence on the climbing height from the source container's free surface to the apex. A one-dimensional theoretical model is developed, taking into account the capillary pressure due to surface tension, pressure loss due to viscous friction, and driving by gravity. Numerical solutions are in good agreement with experiments, and the model suggests hydraulic interpretations for the observed flux dependence on geometrical parameters. The operating principle and characteristics of capillary siphoning revealed here can inform biological phenomena and engineering applications related to directional fluid transport.
JFM classification
Information
- Type
- JFM Rapids
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 9
- Cited by


