Article contents
On turbulent particle fountains
Published online by Cambridge University Press: 23 March 2016
Abstract
We describe new experiments in which particle-laden turbulent fountains with source Froude numbers 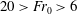 $20>Fr_{0}>6$ are produced when particle-laden fresh water is injected upwards into a reservoir filled with fresh water. We find that the ratio
$20>Fr_{0}>6$ are produced when particle-laden fresh water is injected upwards into a reservoir filled with fresh water. We find that the ratio 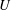 $U$ of the particle fall speed to the characteristic speed of the fountain determines whether the flow is analogous to a single-phase fountain (
$U$ of the particle fall speed to the characteristic speed of the fountain determines whether the flow is analogous to a single-phase fountain ( 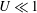 $U\ll 1$ ) or becomes a fully separated flow (
$U\ll 1$ ) or becomes a fully separated flow ( 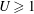 $U\geqslant 1$ ). In the single-phase limit, a fountain with momentum flux
$U\geqslant 1$ ). In the single-phase limit, a fountain with momentum flux 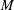 $M$ and buoyancy flux
$M$ and buoyancy flux 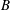 $B$ oscillates about the mean height,
$B$ oscillates about the mean height, 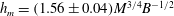 $h_{m}=(1.56\pm 0.04)M^{3/4}B^{-1/2}$ , as fluid periodically cascades from the maximum height,
$h_{m}=(1.56\pm 0.04)M^{3/4}B^{-1/2}$ , as fluid periodically cascades from the maximum height, 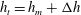 $h_{t}=h_{m}+{\rm\Delta}h$ , to the base of the tank. Experimental measurements of the speed
$h_{t}=h_{m}+{\rm\Delta}h$ , to the base of the tank. Experimental measurements of the speed  $u$ and radius
$u$ and radius  $r$ of the fountain at the mean height
$r$ of the fountain at the mean height 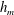 $h_{m}$ , combined with the conservation of buoyancy, suggest that
$h_{m}$ , combined with the conservation of buoyancy, suggest that 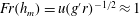 $Fr(h_{m})=u(g^{\prime }r)^{-1/2}\approx 1$ . Using these values, we find that the classical scaling for the frequency of the oscillations,
$Fr(h_{m})=u(g^{\prime }r)^{-1/2}\approx 1$ . Using these values, we find that the classical scaling for the frequency of the oscillations, 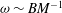 ${\it\omega}\sim BM^{-1}$ , is equivalent to the scaling
${\it\omega}\sim BM^{-1}$ , is equivalent to the scaling 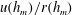 $u(h_{m})/r(h_{m})$ for a fountain supplied at
$u(h_{m})/r(h_{m})$ for a fountain supplied at 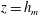 $z=h_{m}$ with
$z=h_{m}$ with 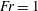 $Fr=1$ (Burridge & Hunt, J. Fluid Mech., vol. 728, 2013, pp. 91–119). This suggests that the oscillations are controlled in the upper part of the fountain where
$Fr=1$ (Burridge & Hunt, J. Fluid Mech., vol. 728, 2013, pp. 91–119). This suggests that the oscillations are controlled in the upper part of the fountain where 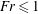 $Fr\leqslant 1$ , and that they may be understood in terms of a balance between the upward supply of a growing dense particle cloud, at the height where
$Fr\leqslant 1$ , and that they may be understood in terms of a balance between the upward supply of a growing dense particle cloud, at the height where 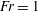 $Fr=1$ , and the downward flow of this cloud. In contrast, in the separated flow regime, we find that particles do not reach the height at which
$Fr=1$ , and the downward flow of this cloud. In contrast, in the separated flow regime, we find that particles do not reach the height at which 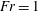 $Fr=1$ : instead, they are transported to the level at which the upward speed of the fountain fluid equals their fall speed. The particles then continuously sediment while the particle-free fountain fluid continues to rise slowly above the height of particle fallout, carried by its momentum.
$Fr=1$ : instead, they are transported to the level at which the upward speed of the fountain fluid equals their fall speed. The particles then continuously sediment while the particle-free fountain fluid continues to rise slowly above the height of particle fallout, carried by its momentum.
JFM classification
Information
- Type
- Rapids
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 15
- Cited by


