Article contents
On the three-dimensional stability of a solid-body rotation flow in a finite-length rotating pipe
Published online by Cambridge University Press: 18 May 2016
Abstract
The three-dimensional, inviscid and viscous flow instability modes that appear on a solid-body rotation flow in a finite-length straight, circular pipe are analysed. This study is a direct extension of the Wang & Rusak (Phys. Fluids, vol. 8 (4), 1996a, pp. 1007–1016) analysis of axisymmetric instabilities on inviscid swirling flows in a pipe. The linear stability equations are the same as those derived by Kelvin (Phil. Mag., vol. 10, 1880, pp. 155–168). However, we study a general mode of perturbation that satisfies the inlet, outlet and wall conditions of a flow in a finite-length pipe with a fixed in time and in space vortex generator ahead of it. This mode is different from the classical normal mode of perturbations. The eigenvalue problem for the growth rate and the shape of the perturbations for any azimuthal wavenumber 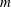 $m$ consists of a linear system of partial differential equations in terms of the axial and radial coordinates (
$m$ consists of a linear system of partial differential equations in terms of the axial and radial coordinates ( 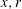 $x,r$ ). The stability problem is solved numerically for all azimuthal wavenumbers
$x,r$ ). The stability problem is solved numerically for all azimuthal wavenumbers 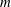 $m$ . The computed growth rates and the related shapes of the various perturbation modes that appear in sequence as a function of the base flow swirl ratio (
$m$ . The computed growth rates and the related shapes of the various perturbation modes that appear in sequence as a function of the base flow swirl ratio ( 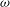 ${\it\omega}$ ) and pipe length (
${\it\omega}$ ) and pipe length ( 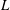 $L$ ) are presented. In the inviscid flow case, the
$L$ ) are presented. In the inviscid flow case, the 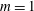 $m=1$ modes are the first to become unstable as the swirl ratio is increased and dominate the perturbation’s growth in a certain range of swirl levels. The
$m=1$ modes are the first to become unstable as the swirl ratio is increased and dominate the perturbation’s growth in a certain range of swirl levels. The 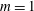 $m=1$ instability modes compete with the axisymmetric (
$m=1$ instability modes compete with the axisymmetric ( 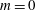 $m=0$ ) instability modes as the swirl ratio is further increased. In the viscous flow case, the viscous damping effects reduce the modes’ growth rates. The neutral stability line is presented in a Reynolds number (
$m=0$ ) instability modes as the swirl ratio is further increased. In the viscous flow case, the viscous damping effects reduce the modes’ growth rates. The neutral stability line is presented in a Reynolds number ( 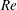 $Re$ ) versus swirl ratio (
$Re$ ) versus swirl ratio ( 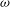 ${\it\omega}$ ) diagram and can be used to predict the first appearance of axisymmetric or spiral instabilities as a function of
${\it\omega}$ ) diagram and can be used to predict the first appearance of axisymmetric or spiral instabilities as a function of 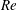 $Re$ and
$Re$ and 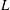 $L$ . We use the Reynolds–Orr equation to analyse the various production terms of the perturbation’s kinetic energy and establish the elimination of the flow axial homogeneity at high swirl levels as the underlying physical mechanism that leads to flow exchange of stability and to the appearance of both spiral and axisymmetric instabilities. The viscous effects in the bulk have only a passive influence on the modes’ shapes and growth rates. These effects decrease with the increase of
$L$ . We use the Reynolds–Orr equation to analyse the various production terms of the perturbation’s kinetic energy and establish the elimination of the flow axial homogeneity at high swirl levels as the underlying physical mechanism that leads to flow exchange of stability and to the appearance of both spiral and axisymmetric instabilities. The viscous effects in the bulk have only a passive influence on the modes’ shapes and growth rates. These effects decrease with the increase of 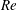 $Re$ . We show that the inviscid flow stability results are the inviscid-limit stability results of high-
$Re$ . We show that the inviscid flow stability results are the inviscid-limit stability results of high- 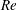 $Re$ rotating flows.
$Re$ rotating flows.
Information
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 22
- Cited by


