Article contents
On the internal flow of a ventilated supercavity
Published online by Cambridge University Press: 16 January 2019
Abstract
This study presents an experimental investigation on the internal flow of a ventilated supercavity using fog flow visualization and particle image velocimetry (PIV) measurements. The ventilated supercavity is generated on a backward-facing cavitator and studied in the high-speed water tunnel at St. Anthony Falls Laboratory. Fog particles are introduced into the supercavity through the ventilation line, and then illuminated by a laser sheet for flow visualizations and PIV measurements. The experiments are performed on the supercavities with two closure types, i.e. the re-entrant jet (RJ) and the twin vortex (TV), under the same water tunnel flow condition but different ventilation rates. The flow visualization revealed three distinct regions within the supercavity, including the ventilation influence region near the cavitator, the extended internal boundary layer along the liquid–gas interface and the reverse flow region occupying a large centre portion of the supercavity. The streamwise and vertical extent of the ventilation influence region, the streamwise growth of the internal boundary layer and the reverse flow within the supercavity are then quantified through PIV flow measurements. Compared to the RJ case, the results indicate that the TV supercavity yields a longer vertical extent of the ventilation influence region, a thinner internal boundary layer and a stronger reverse flow. The internal flow results suggest that at the upstream of the location of the maximum cavity diameter, the gas enters the forward flow (including the internal boundary layer and the forward moving portion of the ventilation influence region) from the reverse flow, while at the downstream of that location, the gas is stripped from the internal boundary layer and enters the reverse flow due to the increasing adverse pressure gradient in the streamwise direction. The above results are combined with visualization results of the supercavity geometry and closure patterns to further explain the influence of gas leakage mechanisms on cavity growth and closure transition. Specifically, visualization of the cavity geometry change during the RJ to TV supercavity transition indicates external flow separation associated with a critical incline angle of the bottom liquid–gas interface at the closure contributes to the onset of RJ closure. The closure visualization shows the coexistence of the toroidal vortex and twin-vortex tubes for the RJ supercavity leads to two gas leakage mechanisms: one associated with the shedding of toroidal vortices (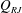 $Q_{RJ}$) and the other due to the gas entrained by the internal boundary layer and leaking from the twin-vortex tubes (
$Q_{RJ}$) and the other due to the gas entrained by the internal boundary layer and leaking from the twin-vortex tubes (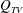 $Q_{TV}$). For the RJ supercavity, with increasing ventilation input, due to the reduction of
$Q_{TV}$). For the RJ supercavity, with increasing ventilation input, due to the reduction of 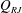 $Q_{RJ}$, the supercavity needs to elongate to increase the gas entrained by the internal boundary layer (i.e.
$Q_{RJ}$, the supercavity needs to elongate to increase the gas entrained by the internal boundary layer (i.e. 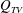 $Q_{TV}$) to balance the ventilation increase. The elongation of the supercavity leads to reduced flow separation, and eventually a transition to the TV supercavity with ventilation above a critical value. For the TV supercavity,
$Q_{TV}$) to balance the ventilation increase. The elongation of the supercavity leads to reduced flow separation, and eventually a transition to the TV supercavity with ventilation above a critical value. For the TV supercavity, 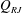 $Q_{RJ}$ is absent. An increase of ventilation input can be balanced by the increase of
$Q_{RJ}$ is absent. An increase of ventilation input can be balanced by the increase of 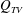 $Q_{TV}$ associated with the widening of the twin-vortex tubes, and therefore, no appreciable elongation of cavity length is observed.
$Q_{TV}$ associated with the widening of the twin-vortex tubes, and therefore, no appreciable elongation of cavity length is observed.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
Wu et al. supplementary movie 1
Supplemental movie showing the far view visualization of the internal flow of RJ supercavity using fog particles.
Wu et al. supplementary movie 2
Supplemental movie showing the close view visualization of the internal flow near the cavitator of RJ supercavity using fog particles.
Wu et al. supplementary movie 3
Supplemental movie showing the far view visualization of the internal flow of TV supercavity using fog particles.
- 89
- Cited by

