Article contents
Nonlinear dynamics of forced baroclinic critical layers
Published online by Cambridge University Press: 25 November 2019
Abstract
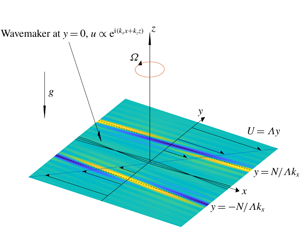
In this paper, we study the forcing of baroclinic critical levels, which arise in stratified fluids with horizontal shear flow along the surfaces where the phase speed of a wave relative to the mean flow matches a natural internal wave speed. Linear theory predicts the baroclinic critical-layer dynamics is similar to that of a classical critical layer, characterized by the secular growth of flow perturbations over a region of decreasing width. By using matched asymptotic expansions, we construct a nonlinear baroclinic critical layer theory to study how the flow perturbations evolve once they enter the nonlinear regime. A key feature of the theory is that, because the location of the baroclinic critical layer is determined by the streamwise wavenumber, the nonlinear dynamics filters out harmonics and the modification to the mean flow controls the evolution. At late times, we show that the vorticity begins to focus into yet smaller regions whose width decreases exponentially with time, and that the addition of dissipative effects can arrest this focussing to create a drifting coherent structure. Jet-like defects in the mean horizontal velocity are the main outcome of the critical-layer dynamics.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 4
- Cited by

