Article contents
Noise generation mechanisms for a supersonic jet impinging on an inclined plate
Published online by Cambridge University Press: 26 May 2016
Abstract
Noise generation mechanisms for a perfectly expanded supersonic Mach number 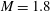 $M=1.8$ turbulent jet impinging on a
$M=1.8$ turbulent jet impinging on a 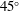 $45^{\circ }$ inclined plate are investigated for a Reynolds number of
$45^{\circ }$ inclined plate are investigated for a Reynolds number of 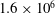 $1.6\times 10^{6}$ employing a large-eddy simulation. Excellent comparisons with experimental acoustic far-field measurements and pressure measurements on the impingement plate are obtained. Two local maxima are identified in the far-field overall sound pressure levels in the
$1.6\times 10^{6}$ employing a large-eddy simulation. Excellent comparisons with experimental acoustic far-field measurements and pressure measurements on the impingement plate are obtained. Two local maxima are identified in the far-field overall sound pressure levels in the 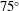 $75^{\circ }$ and
$75^{\circ }$ and 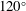 $120^{\circ }$ observer directions, which are associated with different noise generation mechanisms. The peak frequencies in the spectra with Strouhal numbers of
$120^{\circ }$ observer directions, which are associated with different noise generation mechanisms. The peak frequencies in the spectra with Strouhal numbers of 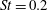 $St=0.2$ for
$St=0.2$ for 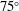 $75^{\circ }$ and
$75^{\circ }$ and 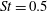 $St=0.5$ for
$St=0.5$ for 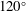 $120^{\circ }$ match the experimental measurements. The jet-impingement region generates pressure waves that propagate predominantly in the
$120^{\circ }$ match the experimental measurements. The jet-impingement region generates pressure waves that propagate predominantly in the 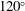 $120^{\circ }$ observer direction. The noise generation in this region is attributed to vortex stretching and tearing during shear-layer impingement, and shock oscillations that are induced by the motion of downstream convected vortical flow structures. The second peak in the overall sound pressure distribution at
$120^{\circ }$ observer direction. The noise generation in this region is attributed to vortex stretching and tearing during shear-layer impingement, and shock oscillations that are induced by the motion of downstream convected vortical flow structures. The second peak in the overall sound pressure distribution at 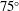 $75^{\circ }$ is associated with noise sources located in the wall jet. The noise generation in the wall jet is associated with supersonically convecting large-scale coherent flow structures that also interact with tail shocks in the wall jet causing large localized pressure fluctuations. Strongly coherent flow structures are identified by applying proper orthogonal decomposition (POD) to the unsteady flow field. The frequency characteristics of the most energetic POD modes are distinctly different based on which energy norm is chosen. The most energetic entropy-based POD modes contain a peak frequency of approximately
$75^{\circ }$ is associated with noise sources located in the wall jet. The noise generation in the wall jet is associated with supersonically convecting large-scale coherent flow structures that also interact with tail shocks in the wall jet causing large localized pressure fluctuations. Strongly coherent flow structures are identified by applying proper orthogonal decomposition (POD) to the unsteady flow field. The frequency characteristics of the most energetic POD modes are distinctly different based on which energy norm is chosen. The most energetic entropy-based POD modes contain a peak frequency of approximately  $St=0.4{-}0.6$ , while the most energetic turbulent kinetic-energy-based POD modes appear to be dominated by lower-frequency content. The causality method, based on Lighthill’s acoustic analogy, is used to link the acoustic noise signature to the relevant physical mechanisms in the source region. A differentiation is made between the application of normalized and non-normalized cross-correlation functions for noise source identification and characterization.
$St=0.4{-}0.6$ , while the most energetic turbulent kinetic-energy-based POD modes appear to be dominated by lower-frequency content. The causality method, based on Lighthill’s acoustic analogy, is used to link the acoustic noise signature to the relevant physical mechanisms in the source region. A differentiation is made between the application of normalized and non-normalized cross-correlation functions for noise source identification and characterization.
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- © Cambridge University Press 2016. This is a work of the U.S. Government and is not subject to copyright protection in the United States.
References
- 59
- Cited by


