Article contents
Motion of a capsule in a curved tube
Published online by Cambridge University Press: 25 November 2020
Abstract
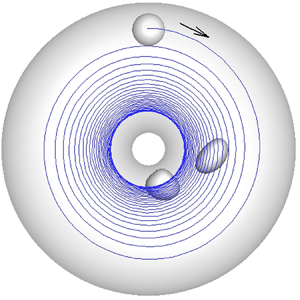
Cross-streamline migration of deformable capsules is studied in three-dimensional curved vessels using a numerical model. Two geometries are chosen: torus vessels to study the effect of constant vessel curvature, and U-shaped vessels to study the effect of change in curvature. A wide range of inertia is considered to include a broad range of applications, from the microcirculation to inertial microfluidics. Vessel curvature and change in curvature are shown to affect capsule migration because of the way they affect the undisturbed flow. In toroidal vessels at negligible inertia, no secondary flow exists and the axial fluid velocity is shifted toward the inner surface of the vessel. In this limit, capsules settle at a location that is away from the vessel centreline, and between the location of the maximum fluid velocity and the innermost surface. Increasing the vessel curvature results in the equilibrium position being increasingly closer to the inner surface. The results suggest the presence of a curvature-induced migration that drives the capsule continuously toward the region of higher streamline curvature. The equilibrium locations are on the symmetry plane of the torus, and are stable equilibria when inertia is negligible. At finite inertia, capsules released on the symmetry plane first settle at an equilibrium located on this plane, which may either be stable or unstable. This equilibrium location depends on both capsule deformability (characterised by capillary number,  $Ca$) and the tube Reynolds number
$Ca$) and the tube Reynolds number  $R{e_t}$. It is closer to the inner edge of the torus for smaller
$R{e_t}$. It is closer to the inner edge of the torus for smaller  $R{e_t}$ and larger
$R{e_t}$ and larger  $Ca$, and toward the outer edge for larger
$Ca$, and toward the outer edge for larger  $R{e_t}$ and smaller
$R{e_t}$ and smaller  $Ca$. This dependence of the equilibria arises due to the secondary flow (or Dean's vortex), which opposes the curvature-induced inward migration. The equilibrium locations on the symmetry plane are unstable if the secondary flow is strong, in which case capsules depart the symmetry plane, and set on to a spiralling motion, eventually settling near the centres of the Dean's vortices. For the U-shaped vessels, the curvature change is shown to create a radial velocity component, even at small inertia, that can be of comparable magnitude to the axial velocity, and that increases with increasing curvature. This radial velocity causes a large and abrupt change in capsule trajectory toward the inner side of the vessel where the curvature increases, but toward the outer side where the curvature decreases.
$Ca$. This dependence of the equilibria arises due to the secondary flow (or Dean's vortex), which opposes the curvature-induced inward migration. The equilibrium locations on the symmetry plane are unstable if the secondary flow is strong, in which case capsules depart the symmetry plane, and set on to a spiralling motion, eventually settling near the centres of the Dean's vortices. For the U-shaped vessels, the curvature change is shown to create a radial velocity component, even at small inertia, that can be of comparable magnitude to the axial velocity, and that increases with increasing curvature. This radial velocity causes a large and abrupt change in capsule trajectory toward the inner side of the vessel where the curvature increases, but toward the outer side where the curvature decreases.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 17
- Cited by


