Article contents
Mixing and reaction in turbulent plumes: the limits of slow and instantaneous chemical kinetics
Published online by Cambridge University Press: 18 December 2018
Abstract
We investigate the behaviour of a reactive plume in the two limiting cases of slow and instantaneous chemical reactions. New laboratory measurements show that, whereas the slow reaction between the source and entrained chemical species takes place within the whole volume of each eddy in the plume, the fast reaction develops preferentially at the periphery of the eddies. We develop a new model that quantifies the mixing of the reactive buoyant fluids at the Batchelor scale and thereby the progress of the fast reaction. We present a series of new experimental results that suggest that a critical distance from the source, 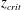 $z_{crit}$, exists at which the volume of fluid that is entrained from the ambient is equal to that which is mixed within the plume at the Batchelor scale. For
$z_{crit}$, exists at which the volume of fluid that is entrained from the ambient is equal to that which is mixed within the plume at the Batchelor scale. For 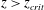 $z>z_{crit}$, only a fraction of the entrained fluid is rapidly mixed and reacts with the plume fluid. The results of the new experiments enable us to quantify the distance from the source at which an instantaneous reaction reaches completion, and show that it can be significantly larger than the distance
$z>z_{crit}$, only a fraction of the entrained fluid is rapidly mixed and reacts with the plume fluid. The results of the new experiments enable us to quantify the distance from the source at which an instantaneous reaction reaches completion, and show that it can be significantly larger than the distance 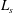 $L_{s}$ at which the stoichiometric dilution of the plume fluid is achieved. In the limit of an instantaneous reaction, the longitudinal profiles of source chemical concentration in the plume depend on
$L_{s}$ at which the stoichiometric dilution of the plume fluid is achieved. In the limit of an instantaneous reaction, the longitudinal profiles of source chemical concentration in the plume depend on  $(z_{crit}/L_{s})^{5/6}$. The predictions of the model are validated against the experimental results, and the profiles of source chemical concentration in the plume for slow and fast reactions are compared.
$(z_{crit}/L_{s})^{5/6}$. The predictions of the model are validated against the experimental results, and the profiles of source chemical concentration in the plume for slow and fast reactions are compared.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 7
- Cited by

