Article contents
Mathematical modelling of thermocapillary patterning in thin liquid film: an equilibrium study
Published online by Cambridge University Press: 26 May 2021
Abstract
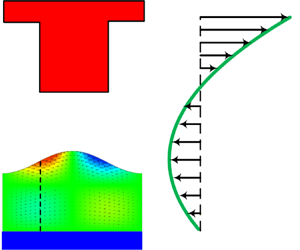
Thermocapillary patterning, namely, the formation of micro/nano patterns in a liquid film by surface deformation induced by an imposed thermal gradient, has enjoyed widespread applications in engineering. In this paper, we present the development of analytical and numerical models and model analyses to predict the equilibrium states of a deformed liquid polymer film under the action of thermocapillary forces. The deformation is found to be dependent on a non-dimensional parameter  $\Im \equiv Ma \, Ca$, with Ma denoting the Marangoni number and Ca the capillary number. Model analyses show that a hysteresis phenomenon is associated with the thermocapillary deformation of the film with increasing and then decreasing
$\Im \equiv Ma \, Ca$, with Ma denoting the Marangoni number and Ca the capillary number. Model analyses show that a hysteresis phenomenon is associated with the thermocapillary deformation of the film with increasing and then decreasing  $\Im$. When
$\Im$. When  $\Im$ is increased above a critical value
$\Im$ is increased above a critical value  ${\Im _{c,1}}$, significant deformation occurs in the film until the polymer touches the top solid template. Then, if
${\Im _{c,1}}$, significant deformation occurs in the film until the polymer touches the top solid template. Then, if  $\Im$ is allowed to decrease, the polymer film would not detach from the template until
$\Im$ is allowed to decrease, the polymer film would not detach from the template until  $\Im$ is decreased below another critical value
$\Im$ is decreased below another critical value  ${\Im _{c,2}}$ (usually
${\Im _{c,2}}$ (usually  ${\Im _{c,2}} < {\Im _{c,1}}$). With
${\Im _{c,2}} < {\Im _{c,1}}$). With  $\Im \in [{\Im _{c,2}},\;{\Im _{c,1}}]$, there exist multiple (three at the maximum) equilibrium states. The Lyapunov energy analysis of these states reveals that one equilibrium state is stable, another is metastable and the third one is unstable.
$\Im \in [{\Im _{c,2}},\;{\Im _{c,1}}]$, there exist multiple (three at the maximum) equilibrium states. The Lyapunov energy analysis of these states reveals that one equilibrium state is stable, another is metastable and the third one is unstable.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 8
- Cited by


