Article contents
The logarithmic variance of streamwise velocity and 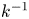 $k^{-1}$ conundrum in wall turbulence
$k^{-1}$ conundrum in wall turbulence
Published online by Cambridge University Press: 20 December 2021
Abstract
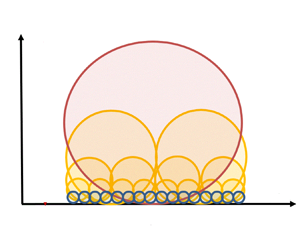
The logarithmic dependence of streamwise turbulence intensity has been observed repeatedly in recent experimental and direct numerical simulation data. However, its spectral counterpart, a well-developed  $k^{-1}$ spectrum (
$k^{-1}$ spectrum ( $k$ is the spatial wavenumber in a wall-parallel direction), has not been convincingly observed from the same data. In the present study, we revisit the spectrum-based attached eddy model of Perry and co-workers, who proposed the emergence of a
$k$ is the spatial wavenumber in a wall-parallel direction), has not been convincingly observed from the same data. In the present study, we revisit the spectrum-based attached eddy model of Perry and co-workers, who proposed the emergence of a  $k^{-1}$ spectrum in the inviscid limit, for small but finite
$k^{-1}$ spectrum in the inviscid limit, for small but finite  $z/\delta$ and for finite Reynolds numbers (
$z/\delta$ and for finite Reynolds numbers ( $z$ is the wall-normal coordinate, and
$z$ is the wall-normal coordinate, and  $\delta$ is the outer length scale). In the upper logarithmic layer (or inertial sublayer), a reexamination reveals that the intensity of the spectrum must vary with the wall-normal location at order of
$\delta$ is the outer length scale). In the upper logarithmic layer (or inertial sublayer), a reexamination reveals that the intensity of the spectrum must vary with the wall-normal location at order of  $z/\delta$, consistent with the early observation argued with ‘incomplete similarity’. The streamwise turbulence intensity is subsequently calculated, demonstrating that the existence of a well-developed
$z/\delta$, consistent with the early observation argued with ‘incomplete similarity’. The streamwise turbulence intensity is subsequently calculated, demonstrating that the existence of a well-developed  $k^{-1}$ spectrum is not a necessary condition for the approximate logarithmic wall-normal dependence of turbulence intensity – a more general condition is the existence of a premultiplied power-spectral intensity of
$k^{-1}$ spectrum is not a necessary condition for the approximate logarithmic wall-normal dependence of turbulence intensity – a more general condition is the existence of a premultiplied power-spectral intensity of  $O(1)$ for
$O(1)$ for  $O(1/\delta ) < k < O(1/z)$. Furthermore, it is shown that the Townsend–Perry constant must be weakly dependent on the Reynolds number. Finally, the analysis is semi-empirically extended to the lower logarithmic layer (or mesolayer), and a near-wall correction for the turbulence intensity is subsequently proposed. All the predictions of the proposed model and the related analyses/assumptions are validated with high-fidelity experimental data (Samie et al., J. Fluid Mech., vol. 851, 2018, pp. 391–415).
$O(1/\delta ) < k < O(1/z)$. Furthermore, it is shown that the Townsend–Perry constant must be weakly dependent on the Reynolds number. Finally, the analysis is semi-empirically extended to the lower logarithmic layer (or mesolayer), and a near-wall correction for the turbulence intensity is subsequently proposed. All the predictions of the proposed model and the related analyses/assumptions are validated with high-fidelity experimental data (Samie et al., J. Fluid Mech., vol. 851, 2018, pp. 391–415).
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 19
- Cited by


