Article contents
Linear global stability of a flow past a sphere under a streamwise magnetic field
Published online by Cambridge University Press: 30 August 2023
Abstract
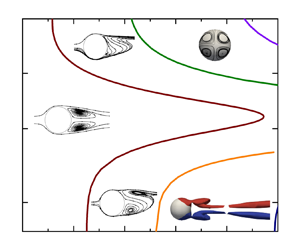
The global linear stability analysis for the magnetohydrodynamic liquid metal flow past an insulated sphere subjected to a constant streamwise magnetic field is investigated in the range of the Reynolds number  $Re\leq 400$ and the interaction number
$Re\leq 400$ and the interaction number  $N\leq 40$ coupled with direct numerical simulations, where
$N\leq 40$ coupled with direct numerical simulations, where  $N$ stands for strength of the electromagnetic force. The stability of the steady axisymmetric base flow to independent time-azimuthal modes is discussed. Five critical curves associated with various wake transitions are obtained in the
$N$ stands for strength of the electromagnetic force. The stability of the steady axisymmetric base flow to independent time-azimuthal modes is discussed. Five critical curves associated with various wake transitions are obtained in the  $\{Re, N\}$ phase diagram. These critical curves reveal the stabilising effect of a weak magnetic field, the destabilising effect of a strong magnetic field and re-stabilising effect of a much stronger magnetic field. To explore the impact of the magnetic field on flow instability, a sensitivity analysis utilizing an adjoint method is performed for the first regular bifurcation. Sensitivity functions of growth rate to base-flow modifications and Lorentz force are defined to identify the region that has the most significant influence on flow instability, such as the recirculation region responsible for the stabilising effect at a weak magnetic field and the shear layer region responsible for the destabilising effect at a strong magnetic field. Furthermore, a competition between the stabilising and shear destabilising effects of the magnetic field is discussed. This analysis provides valuable insights into the non-monotonic effect of the magnetic field on flow instability.
$\{Re, N\}$ phase diagram. These critical curves reveal the stabilising effect of a weak magnetic field, the destabilising effect of a strong magnetic field and re-stabilising effect of a much stronger magnetic field. To explore the impact of the magnetic field on flow instability, a sensitivity analysis utilizing an adjoint method is performed for the first regular bifurcation. Sensitivity functions of growth rate to base-flow modifications and Lorentz force are defined to identify the region that has the most significant influence on flow instability, such as the recirculation region responsible for the stabilising effect at a weak magnetic field and the shear layer region responsible for the destabilising effect at a strong magnetic field. Furthermore, a competition between the stabilising and shear destabilising effects of the magnetic field is discussed. This analysis provides valuable insights into the non-monotonic effect of the magnetic field on flow instability.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
Footnotes
These authors contributed equally to this work and should be considered co-first authors.
References
- 3
- Cited by


