Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
SAITO, Masafumi
and
TAGAWA, Yoshiyuki
2015.
Lift force acting on a levitating drop over a moving wall.
Transactions of the JSME (in Japanese),
Vol. 81,
Issue. 825,
p.
15-00059.
Hale, Jacob
and
Akers, Caleb
2016.
Deceleration of droplets that glide along the free surface of a bath.
Journal of Fluid Mechanics,
Vol. 803,
Issue. ,
p.
313.
Zhu, Lailai
and
Gallaire, François
2016.
A pancake droplet translating in a Hele-Shaw cell: lubrication film and flow field.
Journal of Fluid Mechanics,
Vol. 798,
Issue. ,
p.
955.
Gauthier, Anaïs
Bird, James C.
Clanet, Christophe
and
Quéré, David
2016.
Aerodynamic Leidenfrost effect.
Physical Review Fluids,
Vol. 1,
Issue. 8,
Davanlou, Ashkan
2016.
The Role of Liquid Properties on Lifetime of Levitated Droplets.
Langmuir,
Vol. 32,
Issue. 38,
p.
9736.
Lo, Hau Yung
Liu, Yuan
and
Xu, Lei
2017.
Mechanism of Contact between a Droplet and an Atomically Smooth Substrate.
Physical Review X,
Vol. 7,
Issue. 2,
Zhao, Xi
Tang, Jianbo
and
Liu, Jing
2017.
Surfing liquid metal droplet on the same metal bath via electrolyte interface.
Applied Physics Letters,
Vol. 111,
Issue. 10,
Kreder, Michael J.
Daniel, Dan
Tetreault, Adam
Cao, Zhenle
Lemaire, Baptiste
Timonen, Jaakko V. I.
and
Aizenberg, Joanna
2018.
Film Dynamics and Lubricant Depletion by Droplets Moving on Lubricated Surfaces.
Physical Review X,
Vol. 8,
Issue. 3,
Gauthier, Anaïs
Bouillant, Ambre
Clanet, Christophe
and
Quéré, David
2018.
Aerodynamic repellency of impacting liquids.
Physical Review Fluids,
Vol. 3,
Issue. 5,
Zhao, Xi
Yang, Lixiang
Ding, Yujie
Zhang, Pengju
and
Liu, Jing
2019.
Noncoalescent liquid metal droplets sustained on a magnetic field-circulated liquid metal bath surface.
Applied Physics Letters,
Vol. 115,
Issue. 8,
Shang, Yuheng
Liu, Xiufang
Bai, Bofeng
and
Zhong, Xin
2019.
Central-pointy to central-concave icing transition of an impact droplet by increasing surface subcooling.
International Communications in Heat and Mass Transfer,
Vol. 108,
Issue. ,
p.
104326.
Klamka, Michal
Remer, Michal
and
Bobinski, Tomasz
2019.
Beyond laminar regime – Droplet interaction with air boundary layer.
International Journal of Heat and Mass Transfer,
Vol. 133,
Issue. ,
p.
542.
Law, Kiat Li
and
Chu, Hong-Yu
2019.
Bowling water drops on water surface.
Physics of Fluids,
Vol. 31,
Issue. 6,
Tsai, Meng-Hsien
Law, Kiat Li
and
Chu, Hong-Yu
2019.
Asymmetric vortexes induced traveling drop on an oscillatory liquid bath.
Physics of Fluids,
Vol. 31,
Issue. 10,
Sawaguchi, Erina
Matsuda, Ayumi
Hama, Kai
Saito, Masafumi
and
Tagawa, Yoshiyuki
2019.
Droplet levitation over a moving wall with a steady air film.
Journal of Fluid Mechanics,
Vol. 862,
Issue. ,
p.
261.
Hale, Jacob
and
Boudreau, Jacob
2019.
Scattering of liquid droplets from axisymmetric targets.
Physical Review Fluids,
Vol. 4,
Issue. 3,
Shukla, Isha
Kofman, Nicolas
Balestra, Gioele
Zhu, Lailai
and
Gallaire, François
2019.
Film thickness distribution in gravity-driven pancake-shaped droplets rising in a Hele-Shaw cell.
Journal of Fluid Mechanics,
Vol. 874,
Issue. ,
p.
1021.
Mogilevskiy, E.
2020.
Levitation of a nonboiling droplet over hot liquid bath.
Physics of Fluids,
Vol. 32,
Issue. 1,
Dong, Teng
Wang, Fei
Weheliye, Weheliye H.
and
Angeli, Panagiota
2020.
Surfing of drops on moving liquid–liquid interfaces.
Journal of Fluid Mechanics,
Vol. 892,
Issue. ,
Dalwadi, Mohit P.
Cimpeanu, Radu
Ockendon, Hilary
Ockendon, John
and
Mullin, Tom
2021.
Levitation of a cylinder by a thin viscous film.
Journal of Fluid Mechanics,
Vol. 917,
Issue. ,
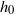 ${h}_{0} $ : for large drops
${h}_{0} $ : for large drops 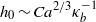 ${h}_{0} \sim {\mathit{Ca}}^{2/ 3} { \kappa }_{b}^{- 1} $ , as in the Bretherton problem, where
${h}_{0} \sim {\mathit{Ca}}^{2/ 3} { \kappa }_{b}^{- 1} $ , as in the Bretherton problem, where  $\mathit{Ca}$ is the capillary number based on the air viscosity and
$\mathit{Ca}$ is the capillary number based on the air viscosity and 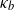 ${\kappa }_{b} $ is the curvature at the bottom of the drop; for small drops
${\kappa }_{b} $ is the curvature at the bottom of the drop; for small drops  ${h}_{0} \sim {\mathit{Ca}}^{4/ 5} {(a{\kappa }_{b} )}^{4/ 5} { \kappa }_{b}^{- 1} $ , where
${h}_{0} \sim {\mathit{Ca}}^{4/ 5} {(a{\kappa }_{b} )}^{4/ 5} { \kappa }_{b}^{- 1} $ , where  $a$ is the capillary length.
$a$ is the capillary length.
