No CrossRef data available.
Published online by Cambridge University Press: 26 April 2021
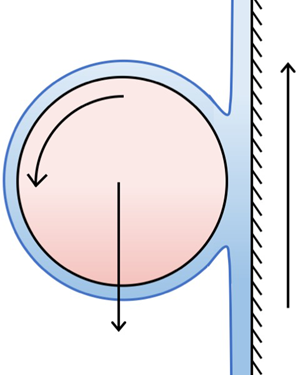
When a horizontal cylinder is placed on a vertically moving belt coated with a thin layer of viscous fluid, experiments reveal that, at a specific belt velocity, the cylinder can be levitated at a fixed height while rotating around its own axis at an a priori unknown rate. We develop and solve a model for this experiment, using a combination of asymptotic analysis and direct numerical simulation. We obtain a relationship between the belt speed and cylinder rotation rate, which we successfully compare with experimental results.
A real-time video (24 FPS) of the cylinder levitation experiment described in Section 2 and shown in Figure 1, as viewed from the front. The aluminium cylinder has a diameter of 13 mm and a length of 15 mm. The belt width is 26.5 mm and the film thickness is 0.3 mm.
A real-time video (24 FPS) of the cylinder levitation experiment described in Section 2 and shown in Figure 1, as viewed from the side. The aluminium cylinder has a diameter of 8 mm and a length of 15 mm. The belt width is 26.5 mm and the film thickness is 0.3 mm.
Animation summary of the direct numerical simulation (DNS) framework designed for the inner problem (described in subsections 4.2 and 4.3) accompanying figure 7 of the manuscript. Illustrated are, in sequence, the two fluids with explanatory notes, followed by the pressure and velocity field norm, and finally the horizontal and vertical velocity component contributions. The relevant dimensionless flow parameters are $Ca = 2.0$, $U = 1.0$, and $\Omega = 0.6$, with the underlying dimensional quantities described in section 2 as part of the experimental set-up.