Article contents
Generation of attached Langmuir circulations by a suspended macroalgal farm
Published online by Cambridge University Press: 19 March 2021
Abstract
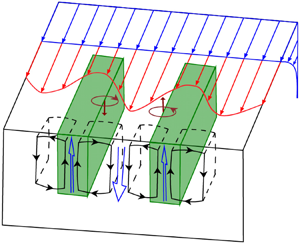
In this study, we focus on Langmuir turbulence in the deep ocean with the presence of a large macroalgal farm using a large eddy simulation method. The wave–current interactions are modelled by solving the wave-averaged equations. The hydrodynamic process over the farm is found to drive a persistent flow pattern similar to Langmuir circulations but is locked in space across the farm. These secondary circulations are generated because the cross-stream shear produced by the rows of canopy elements leads to a steady vertical vorticity field, which is then rotated to the downstream direction under the effect of vortex force. Since the driving mechanism is similar to the Craik–Leibovich type 2 instability theory, these secondary circulations are also termed as attached Langmuir circulations. We then apply a triple decomposition on the flow field to unveil the underlying kinematics and energy transfer between the mean flow, the secondary flow resulting from the farm drag and the transient eddies. Flow visualizations and statistics suggest that the attached Langmuir circulations result from the adjustment of the upper ocean mixed layer to the macroalgal farm, and they will weaken (if not disappear) when the flow reaches an equilibrium state within the farm. The triple-decomposed energy budgets reveal that the energy of the secondary flow is transferred from the mean flow under the action of canopy drag, while the transient eddies feed on wave energy transferred by the Stokes drift and energy conversion from the secondary flow.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 10
- Cited by


