Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zhao, Ming
Cheng, Liang
and
Lu, Lin
2014.
Vortex induced vibrations of a rotating circular cylinder at low Reynolds number.
Physics of Fluids,
Vol. 26,
Issue. 7,
Wang, Huakun
Zhao, Dongliang
Yang, Wenyu
and
Yu, Guoliang
2015.
Numerical investigation on flow-induced vibration of a triangular cylinder at a low Reynolds number.
Fluid Dynamics Research,
Vol. 47,
Issue. 1,
p.
015501.
Seyed-Aghazadeh, Banafsheh
and
Modarres-Sadeghi, Yahya
2015.
An experimental investigation of vortex-induced vibration of a rotating circular cylinder in the crossflow direction.
Physics of Fluids,
Vol. 27,
Issue. 6,
Zhao, Ming
2015.
Numerical simulation of vortex-induced vibration of a circular cylinder in a spanwise shear flow.
Physics of Fluids,
Vol. 27,
Issue. 6,
Bourguet, Rémi
and
Lo Jacono, David
2015.
In-line flow-induced vibrations of a rotating cylinder.
Journal of Fluid Mechanics,
Vol. 781,
Issue. ,
p.
127.
Seyed-Aghazadeh, Banafsheh
and
Modarres-Sadeghi, Yahya
2016.
Reconstructing the vortex-induced-vibration response of flexible cylinders using limited localized measurement points.
Journal of Fluids and Structures,
Vol. 65,
Issue. ,
p.
433.
Bauerheim, M.
Ndiaye, A.
Constantine, P.
Moreau, S.
and
Nicoud, F.
2016.
Symmetry breaking of azimuthal thermoacoustic modes: the UQ perspective.
Journal of Fluid Mechanics,
Vol. 789,
Issue. ,
p.
534.
Zhao, Ming
Cui, Zhendong
Kwok, Kenny
and
Zhang, Yu
2016.
Wake-induced vibration of a small cylinder in the wake of a large cylinder.
Ocean Engineering,
Vol. 113,
Issue. ,
p.
75.
Zhao, Ming
Kaja, Kalyani
Xiang, Yang
and
Cheng, Liang
2016.
Vortex-induced vibration of four cylinders in an in-line square configuration.
Physics of Fluids,
Vol. 28,
Issue. 2,
Zhao, Ming
Murphy, Joshua M.
and
Kwok, Kenny
2016.
Numerical Simulation of Vortex-Induced Vibration of Two Rigidly Connected Cylinders in Side-by-Side and Tandem Arrangements Using RANS Model.
Journal of Fluids Engineering,
Vol. 138,
Issue. 2,
Wong, K. W. L.
Zhao, J.
Lo Jacono, D.
Thompson, M. C.
and
Sheridan, J.
2017.
Experimental investigation of flow-induced vibration of a rotating circular cylinder.
Journal of Fluid Mechanics,
Vol. 829,
Issue. ,
p.
486.
Wang, Zhuo
Du, Lin
Zhao, Jisheng
and
Sun, Xiaofeng
2017.
Structural response and energy extraction of a fully passive flapping foil.
Journal of Fluids and Structures,
Vol. 72,
Issue. ,
p.
96.
Alam, Md. Mahbub
Zheng, Qinmin
and
Hourigan, Kerry
2017.
The wake and thrust by four side-by-side cylinders at a low Re.
Journal of Fluids and Structures,
Vol. 70,
Issue. ,
p.
131.
Mejia, D.
Bauerheim, M.
Xavier, P.
Ferret, B.
Selle, L.
and
Poinsot, T.
2017.
Stabilization of a premixed laminar flame on a rotating cylinder.
Proceedings of the Combustion Institute,
Vol. 36,
Issue. 1,
p.
1447.
Xavier, P.
Ghani, A.
Mejia, D.
Miguel-Brebion, M.
Bauerheim, M.
Selle, L.
and
Poinsot, T.
2017.
Experimental and numerical investigation of flames stabilised behind rotating cylinders: interaction of flames with a moving wall.
Journal of Fluid Mechanics,
Vol. 813,
Issue. ,
p.
127.
Gsell, Simon
Bourguet, Rémi
and
Braza, Marianna
2017.
Vortex-induced vibrations of a cylinder in planar shear flow.
Journal of Fluid Mechanics,
Vol. 825,
Issue. ,
p.
353.
Teymourtash, A. R.
and
Salimipour, S. E.
2017.
Compressibility effects on the flow past a rotating cylinder.
Physics of Fluids,
Vol. 29,
Issue. 1,
Vicente-Ludlam, D.
Barrero-Gil, A.
and
Velazquez, A.
2017.
Flow-Induced Vibration of a rotating circular cylinder using position and velocity feedback.
Journal of Fluids and Structures,
Vol. 72,
Issue. ,
p.
127.
Gao, Yun
Zong, Zhi
Zou, Li
Takagi, Shu
and
Jiang, Zongyu
2018.
Numerical simulation of vortex-induced vibration of a circular cylinder with different surface roughnesses.
Marine Structures,
Vol. 57,
Issue. ,
p.
165.
Chen, Weilin
Ji, Chunning
Williams, John
Xu, Dong
Yang, Lihong
and
Cui, Yuting
2018.
Vortex-induced vibrations of three tandem cylinders in laminar cross-flow: Vibration response and galloping mechanism.
Journal of Fluids and Structures,
Vol. 78,
Issue. ,
p.
215.
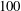 $100$, based on the cylinder diameter and inflow velocity. The cylinder is found to oscillate freely up to a rotation rate (ratio between the cylinder surface and inflow velocities) close to
$100$, based on the cylinder diameter and inflow velocity. The cylinder is found to oscillate freely up to a rotation rate (ratio between the cylinder surface and inflow velocities) close to 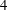 $4$. Under forced rotation, the vibration amplitude exhibits a bell-shaped evolution as a function of the reduced velocity (inverse of the oscillator natural frequency) and reaches
$4$. Under forced rotation, the vibration amplitude exhibits a bell-shaped evolution as a function of the reduced velocity (inverse of the oscillator natural frequency) and reaches 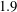 $1.9$ diameters, i.e. three times the maximum amplitude in the non-rotating case. The free vibrations of the rotating cylinder occur under a condition of wake–body synchronization similar to the lock-in condition driving non-rotating cylinder VIV. The largest vibration amplitudes are associated with a novel asymmetric wake pattern composed of a triplet of vortices and a single vortex shed per cycle, the
$1.9$ diameters, i.e. three times the maximum amplitude in the non-rotating case. The free vibrations of the rotating cylinder occur under a condition of wake–body synchronization similar to the lock-in condition driving non-rotating cylinder VIV. The largest vibration amplitudes are associated with a novel asymmetric wake pattern composed of a triplet of vortices and a single vortex shed per cycle, the  ${\rm T} + {\rm S}$ pattern. In the low-frequency vibration regime, the flow exhibits another new topology, the U pattern, characterized by a transverse undulation of the spanwise vorticity layers without vortex detachment; consequently, free oscillations of the rotating cylinder may also develop in the absence of vortex shedding. The symmetry breaking due to the rotation is shown to directly impact the selection of the higher harmonics appearing in the fluid force spectra. The rotation also influences the mechanism of phasing between the force and the structural response.
${\rm T} + {\rm S}$ pattern. In the low-frequency vibration regime, the flow exhibits another new topology, the U pattern, characterized by a transverse undulation of the spanwise vorticity layers without vortex detachment; consequently, free oscillations of the rotating cylinder may also develop in the absence of vortex shedding. The symmetry breaking due to the rotation is shown to directly impact the selection of the higher harmonics appearing in the fluid force spectra. The rotation also influences the mechanism of phasing between the force and the structural response.
