Article contents
Flow-induced vibrations of a rotating cylinder in an arbitrary direction
Published online by Cambridge University Press: 11 December 2018
Abstract
The flow-induced vibrations of an elastically mounted circular cylinder, free to oscillate in an arbitrary direction and forced to rotate about its axis, are examined via two- and three-dimensional simulations, at a Reynolds number equal to 100, based on the body diameter and inflow velocity. The behaviour of the flow–structure system is investigated over the entire range of vibration directions, defined by the angle 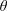 $\unicode[STIX]{x1D703}$ between the direction of the current and the direction of motion, a wide range of values of the reduced velocity
$\unicode[STIX]{x1D703}$ between the direction of the current and the direction of motion, a wide range of values of the reduced velocity 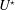 $U^{\star }$ (inverse of the oscillator natural frequency) and three values of the rotation rate (ratio between the cylinder surface and inflow velocities),
$U^{\star }$ (inverse of the oscillator natural frequency) and three values of the rotation rate (ratio between the cylinder surface and inflow velocities), 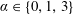 $\unicode[STIX]{x1D6FC}\in \{0,1,3\}$, in order to cover the reference non-rotating cylinder case, as well as typical slow and fast rotation cases. The oscillations of the non-rotating cylinder (
$\unicode[STIX]{x1D6FC}\in \{0,1,3\}$, in order to cover the reference non-rotating cylinder case, as well as typical slow and fast rotation cases. The oscillations of the non-rotating cylinder (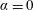 $\unicode[STIX]{x1D6FC}=0$) develop under wake-body synchronization or lock-in, and their amplitude exhibits a bell-shaped evolution, typical of vortex-induced vibrations (VIV), as a function of
$\unicode[STIX]{x1D6FC}=0$) develop under wake-body synchronization or lock-in, and their amplitude exhibits a bell-shaped evolution, typical of vortex-induced vibrations (VIV), as a function of 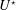 $U^{\star }$. When
$U^{\star }$. When 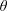 $\unicode[STIX]{x1D703}$ is increased from
$\unicode[STIX]{x1D703}$ is increased from 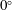 $0^{\circ }$ to
$0^{\circ }$ to 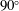 $90^{\circ }$ (or decreased from
$90^{\circ }$ (or decreased from 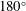 $180^{\circ }$ to
$180^{\circ }$ to 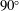 $90^{\circ }$), the bell-shaped curve tends to monotonically increase in width and magnitude. For all angles, the flow past the non-rotating body is two-dimensional with formation of two counter-rotating spanwise vortices per cycle. The behaviour of the system remains globally the same for
$90^{\circ }$), the bell-shaped curve tends to monotonically increase in width and magnitude. For all angles, the flow past the non-rotating body is two-dimensional with formation of two counter-rotating spanwise vortices per cycle. The behaviour of the system remains globally the same for  $\unicode[STIX]{x1D6FC}=1$. The principal effects of the slow rotation are a slight amplification of the VIV-like responses and widening of the vibration windows, as well as a limited asymmetry of the responses and forces about the symmetrical configuration
$\unicode[STIX]{x1D6FC}=1$. The principal effects of the slow rotation are a slight amplification of the VIV-like responses and widening of the vibration windows, as well as a limited asymmetry of the responses and forces about the symmetrical configuration 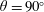 $\unicode[STIX]{x1D703}=90^{\circ }$. The impact of the fast rotation (
$\unicode[STIX]{x1D703}=90^{\circ }$. The impact of the fast rotation (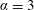 $\unicode[STIX]{x1D6FC}=3$) is more pronounced: VIV-like responses persist over a range of
$\unicode[STIX]{x1D6FC}=3$) is more pronounced: VIV-like responses persist over a range of 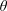 $\unicode[STIX]{x1D703}$ but, outside this range, the system is found to undergo a transition towards galloping-like oscillations characterised by amplitudes growing unboundedly with
$\unicode[STIX]{x1D703}$ but, outside this range, the system is found to undergo a transition towards galloping-like oscillations characterised by amplitudes growing unboundedly with 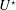 $U^{\star }$. A quasi-steady modelling of fluid forcing predicts the emergence of galloping-like responses as
$U^{\star }$. A quasi-steady modelling of fluid forcing predicts the emergence of galloping-like responses as 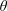 $\unicode[STIX]{x1D703}$ is varied, which suggests that they could be mainly driven by the mean flow. It, however, appears that flow unsteadiness and body motion remain synchronised in this vibration regime where a variety of multi-vortex wake patterns are uncovered. The interaction with flow dynamics results in deviations from the quasi-steady prediction. The successive steps in the evolution of the vibration amplitude versus
$\unicode[STIX]{x1D703}$ is varied, which suggests that they could be mainly driven by the mean flow. It, however, appears that flow unsteadiness and body motion remain synchronised in this vibration regime where a variety of multi-vortex wake patterns are uncovered. The interaction with flow dynamics results in deviations from the quasi-steady prediction. The successive steps in the evolution of the vibration amplitude versus 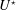 $U^{\star }$, linked to wake pattern switch, are not captured by the quasi-steady approach. The flow past the rapidly-rotating, vibrating cylinder becomes three-dimensional over an interval of
$U^{\star }$, linked to wake pattern switch, are not captured by the quasi-steady approach. The flow past the rapidly-rotating, vibrating cylinder becomes three-dimensional over an interval of 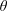 $\unicode[STIX]{x1D703}$ including the in-line oscillation configuration, with only a minor effect on the system behaviour.
$\unicode[STIX]{x1D703}$ including the in-line oscillation configuration, with only a minor effect on the system behaviour.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 27
- Cited by

