Article contents
Fast Stokesian dynamics
Published online by Cambridge University Press: 17 September 2019
Abstract
We present a new method for large scale dynamic simulation of colloidal particles with hydrodynamic interactions and Brownian forces, which we call fast Stokesian dynamics (FSD). The approach for modelling the hydrodynamic interactions between particles is based on the Stokesian dynamics (SD) algorithm (J. Fluid Mech., vol. 448, 2001, pp. 115–146), which decomposes the interactions into near-field (short-ranged, pairwise additive and diverging) and far-field (long-ranged many-body) contributions. In FSD, the standard system of linear equations for SD is reformulated using a single saddle point matrix. We show that this reformulation is generalizable to a host of particular simulation methods enabling the self-consistent inclusion of a wide range of constraints, geometries and physics in the SD simulation scheme. Importantly for fast, large scale simulations, we show that the saddle point equation is solved very efficiently by iterative methods for which novel preconditioners are derived. In contrast to existing approaches to accelerating SD algorithms, the FSD algorithm avoids explicit inversion of ill-conditioned hydrodynamic operators without adequate preconditioning, which drastically reduces computation time. Furthermore, the FSD formulation is combined with advanced sampling techniques in order to rapidly generate the stochastic forces required for Brownian motion. Specifically, we adopt the standard approach of decomposing the stochastic forces into near-field and far-field parts. The near-field Brownian force is readily computed using an iterative Krylov subspace method, for which a novel preconditioner is developed, while the far-field Brownian force is efficiently computed by linearly transforming those forces into a fluctuating velocity field, computed easily using the positively split Ewald approach (J. Chem. Phys., vol. 146, 2017, 124116). The resultant effect of this field on the particle motion is determined through solution of a system of linear equations using the same saddle point matrix used for deterministic calculations. Thus, this calculation is also very efficient. Additionally, application of the saddle point formulation to develop high-resolution hydrodynamic models from constrained collections of particles (similar to the immersed boundary method) is demonstrated and the convergence of such models is discussed in detail. Finally, an optimized graphics processing unit implementation of FSD for mono-disperse spherical particles is used to demonstrated performance and accuracy of dynamic simulations of 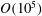 $O(10^{5})$ particles, and an open source plugin for the HOOMD-blue suite of molecular dynamics software is included in the supplementary material.
$O(10^{5})$ particles, and an open source plugin for the HOOMD-blue suite of molecular dynamics software is included in the supplementary material.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 59
- Cited by

