Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Guerrero, Byron
Lambert, Martin F.
and
Chin, Rey C.
2021.
Transient dynamics of accelerating turbulent pipe flow.
Journal of Fluid Mechanics,
Vol. 917,
Issue. ,
Yang, Xiang I. A.
Hong, Jiarong
Lee, Myoungkyu
and
Huang, Xinyi L. D.
2021.
Grid resolution requirement for resolving rare and high intensity wall-shear stress events in direct numerical simulations.
Physical Review Fluids,
Vol. 6,
Issue. 5,
Ng, Henry C.-H.
Collignon, Emile
Poole, Robert J.
and
Dennis, David J. C.
2021.
Energetic motions in turbulent partially filled pipe flow.
Physics of Fluids,
Vol. 33,
Issue. 2,
Chen, Tao
Liu, Tianshu
and
Wang, Lian-Ping
2021.
Features of surface physical quantities and temporal-spatial evolution of wall-normal enstrophy flux in wall-bounded flows.
Physics of Fluids,
Vol. 33,
Issue. 12,
Ivashchenko, V A
Zaripov, D I
and
Mullyadzhanov, R I
2021.
The effect of Reynolds number on near-wall reverse flow in a turbulent duct flow.
Journal of Physics: Conference Series,
Vol. 2119,
Issue. 1,
p.
012032.
Zaripov, Dinar
Ivashchenko, Vladislav
Mullyadzhanov, Rustam
Li, Renfu
Markovich, Dmitriy
and
Kähler, Christian J.
2021.
Reverse flow phenomenon in duct corners at a low Reynolds number.
Physics of Fluids,
Vol. 33,
Issue. 8,
Chen, Tao
Liu, Tianshu
Dong, Zhi-Qiang
Wang, Lian-Ping
and
Chen, Shiyi
2021.
Near-wall flow structures and related surface quantities in wall-bounded turbulence.
Physics of Fluids,
Vol. 33,
Issue. 6,
Chen, Xue
Chung, Yongmann M.
and
Wan, Minping
2021.
The uniform-momentum zones and internal shear layers in turbulent pipe flows at Reynolds numbers up to Reτ=1000.
International Journal of Heat and Fluid Flow,
Vol. 90,
Issue. ,
p.
108817.
Yuan, Xianxu
Tong, Fulin
Li, Weipeng
Chen, Jianqiang
and
Dong, Siwei
2022.
Wall-attached temperature structures in supersonic turbulent boundary layers.
Physics of Fluids,
Vol. 34,
Issue. 11,
Tong, Fulin
Dong, Siwei
Duan, Junyi
Yuan, Xianxu
and
Li, Xinliang
2022.
Effect of expansion on the wall heat flux in a supersonic turbulent boundary layer.
Physics of Fluids,
Vol. 34,
Issue. 10,
Tong, Fulin
Dong, Siwei
Lai, Jiang
Yuan, Xianxu
and
Li, Xinliang
2022.
Wall shear stress and wall heat flux in a supersonic turbulent boundary layer.
Physics of Fluids,
Vol. 34,
Issue. 1,
Dong, Siwei
Tong, Fulin
Yu, Ming
Chen, Jianqiang
Yuan, Xianxu
and
Wang, Qian
2022.
Positive and negative pairs of fluctuating wall shear stress and heat flux in supersonic turbulent boundary layers.
Physics of Fluids,
Vol. 34,
Issue. 8,
Guerrero, Byron
Lambert, Martin F.
and
Chin, Rey C.
2022.
Precursors of backflow events and their relationship with the near-wall self-sustaining process.
Journal of Fluid Mechanics,
Vol. 933,
Issue. ,
Ruby, Marius
and
Foysi, Holger
2022.
Active control of compressible channel flow up to Mab=3 using direct numerical simulations with spanwise velocity modulation at the walls.
GAMM-Mitteilungen,
Vol. 45,
Issue. 1,
Cheng, Cheng
and
Fu, Lin
2022.
Consistency between the attached-eddy model and the inner–outer interaction model: a study of streamwise wall-shear stress fluctuations in a turbulent channel flow.
Journal of Fluid Mechanics,
Vol. 942,
Issue. ,
Chen, Tao
and
Liu, Tianshu
2022.
Near-wall Taylor-series expansion solution for compressible Navier–Stokes–Fourier system.
AIP Advances,
Vol. 12,
Issue. 1,
Guerrero, Byron
Lambert, Martin F.
and
Chin, Rey C.
2022.
Extension of the 1D Unsteady Friction Model for Rapidly Accelerating and Decelerating Turbulent Pipe Flows.
Journal of Hydraulic Engineering,
Vol. 148,
Issue. 9,
Dong, Siwei
Tong, Fulin
Yu, Ming
Chen, Jianqiang
Yuan, Xianxu
and
Wang, Qian
2022.
Effects of wall temperature on two-point statistics of the fluctuating wall shear stress and heat flux in supersonic turbulent boundary layers.
Physics of Fluids,
Vol. 34,
Issue. 6,
2023.
Lie derivatives of fundamental surface quantities in incompressible viscous flows.
Physics of Fluids,
Vol. 35,
Issue. 5,
DUAN, Junyi
TONG, Fulin
LI, Xinliang
and
LIU, Hongwei
2023.
Decomposition of mean skin friction in incident shock wave/turbulent boundary layer interaction flows at Mach 2.25.
Chinese Journal of Aeronautics,
Vol. 36,
Issue. 9,
p.
178.
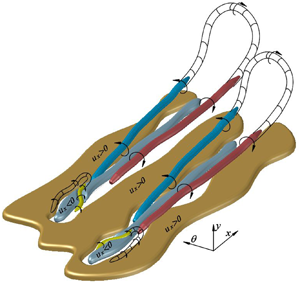
 $\textit {Re}_{\tau} \approx 1000$. The results reveal that extreme positive wall-friction events are located below an intense sweep (Q4) event originated from a strong quasi-streamwise vortex at the buffer region. This vortex transports high streamwise momentum from the overlap and the outer layers towards the wall, giving rise to a high-speed streak within the inner region. This vortical structure also relates to regions with extreme wall-normal velocity. Consequently, the conditional fields of turbulence production and viscous dissipation exhibit peaks whose magnitudes are approximately 25 times higher than the ensemble mean quantities in the vicinity of the extreme positive events. An analysis of the turbulent inertia force reveals that the energetic quasi-streamwise vortex acts as an essential source of momentum at the near-wall region. Similarly, extremely rare backflow events are studied. An examination of the wall-normal vorticity and velocity vector fields shows an identifiable oblique vortical structure along with two other large-scale roll modes. These counter-rotating motions contribute to the formation of backflow events by transporting streamwise momentum from the inner to the outer region, creating a large-scale meandering low-speed streak. It is found that extreme events are clustered below large-scale structures of positive streamwise momentum that interact with near-wall low-speed streaks, related to regions densely populated with vortical structures. Finally, a three-dimensional model is proposed to conceptualise the flow dynamics associated with extreme events.
$\textit {Re}_{\tau} \approx 1000$. The results reveal that extreme positive wall-friction events are located below an intense sweep (Q4) event originated from a strong quasi-streamwise vortex at the buffer region. This vortex transports high streamwise momentum from the overlap and the outer layers towards the wall, giving rise to a high-speed streak within the inner region. This vortical structure also relates to regions with extreme wall-normal velocity. Consequently, the conditional fields of turbulence production and viscous dissipation exhibit peaks whose magnitudes are approximately 25 times higher than the ensemble mean quantities in the vicinity of the extreme positive events. An analysis of the turbulent inertia force reveals that the energetic quasi-streamwise vortex acts as an essential source of momentum at the near-wall region. Similarly, extremely rare backflow events are studied. An examination of the wall-normal vorticity and velocity vector fields shows an identifiable oblique vortical structure along with two other large-scale roll modes. These counter-rotating motions contribute to the formation of backflow events by transporting streamwise momentum from the inner to the outer region, creating a large-scale meandering low-speed streak. It is found that extreme events are clustered below large-scale structures of positive streamwise momentum that interact with near-wall low-speed streaks, related to regions densely populated with vortical structures. Finally, a three-dimensional model is proposed to conceptualise the flow dynamics associated with extreme events.