Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bhat, S. S.
Zhao, J.
Sheridan, J.
Hourigan, K.
and
Thompson, M. C.
2019.
Aspect ratio studies on insect wings.
Physics of Fluids,
Vol. 31,
Issue. 12,
Arias, F.J.
2020.
Ferrofluid thin films for aerofoil lift enhancement and delaying flow separation.
The Aeronautical Journal,
Vol. 124,
Issue. 1282,
p.
1865.
Liu, Chao
Li, Pengpeng
Song, Fa
and
Sun, Jiyu
2021.
Wing shape optimization design inspired by beetle hindwings in wind tunnel experiments.
Computers in Biology and Medicine,
Vol. 135,
Issue. ,
p.
104642.
Dong, Yifeng
Yao, Xuefeng
and
Xu, Xiaoyao
2021.
Cross section shape optimization design of fabric rubber seal.
Composite Structures,
Vol. 256,
Issue. ,
p.
113047.
Engels, Thomas
Kolomenskiy, Dmitry
and
Lehmann, Fritz-Olaf
2021.
Flight efficiency is a key to diverse wing morphologies in small insects.
Journal of The Royal Society Interface,
Vol. 18,
Issue. 183,
Ghanbarzadeh-Dagheyan, Ashkan
Jalili, Nader
and
Ahmadian, Mohammad Taghi
2021.
A holistic survey on mechatronic Systems in Micro/Nano scale with challenges and applications.
Journal of Micro-Bio Robotics,
Vol. 17,
Issue. 1,
p.
1.
Li, Hao
and
Nabawy, Mostafa R. A.
2022.
Effects of Stroke Amplitude and Wing Planform on the Aerodynamic Performance of Hovering Flapping Wings.
Aerospace,
Vol. 9,
Issue. 9,
p.
479.
Bhat, Shantanu S.
and
Thompson, Mark C.
2022.
Effect of leading-edge curvature on the aerodynamics of insect wings.
International Journal of Heat and Fluid Flow,
Vol. 93,
Issue. ,
p.
108898.
Sabeti, Mohammad Hassan
Ezabadi, Mostafa
Banazadeh, Afshin
Saghafi, Fariborz
and
Emami, Seyyed Ali
2023.
Equivalent Linear Model Identification and Periodic Control of a Mono-Wing Aerial Vehicle.
Journal of Intelligent & Robotic Systems,
Vol. 108,
Issue. 4,
Wang, Luyao
Chen, Long
and
Wang, Yanqing
2023.
Proceedings of 2022 International Conference on Autonomous Unmanned Systems (ICAUS 2022).
Vol. 1010,
Issue. ,
p.
358.
Huang, Qiuxiang
Bhat, Shantanu S.
Yeo, Eng Chow
Young, John
Lai, Joseph C.S.
Tian, Fang-Bao
and
Ravi, Sridhar
2023.
Power synchronisations determine the hovering flight efficiency of passively pitching flapping wings.
Journal of Fluid Mechanics,
Vol. 974,
Issue. ,
Wang, Luyao
and
Wang, Yan Qing
2024.
Aerodynamic optimization of a micro flapping rotary wing in hovering flight.
Acta Mechanica,
Vol. 235,
Issue. 8,
p.
5357.
Wu, Guilin
Deng, Shuanghou
and
Li, Qingxi
2024.
Influence of Area Distribution Along the Span Direction on Flapping Wing Aerodynamics in Hover Based on Numerical Modeling Analysis.
IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,
Vol. 17,
Issue. ,
p.
6683.
Addo-Akoto, Reynolds
Han, Jong-Seob
and
Han, Jae-Hung
2024.
Leading-edge curvature effect on aerodynamic performance of flapping wings in hover and forward flight.
Bioinspiration & Biomimetics,
Vol. 19,
Issue. 5,
p.
056007.
Addo-Akoto, Reynolds
Han, Jae-Hung
and
Han, Jong-Seob
2024.
Leading-Edge Curvature Effect on Flapping Performance of Low Aspect Ratio Wings in Forward Flight.
Mou, Ruiyong
Li, Zhe
Huang, Xingrong
Huang, Wei-Xi
and
Fang, Le
2025.
Shape optimization of a flexible flapping wing with hovering
kinematics.
Physics of Fluids,
Vol. 37,
Issue. 3,
Kwon, Hyun Ki
and
Chang, Jo Won
2025.
Effects of shapes and kinematics of hovering flapping wings on aerodynamic forces and vortex structures.
Scientific Reports,
Vol. 15,
Issue. 1,
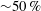 ${\sim}50\,\%$) than the initial rectangular wing forebear. Interestingly, the optimised shapes are found to have a large area outboard, broadly in line with the features of high-lift forewings of multi-winged insects. According to specific aerodynamic performance requirements, this novel method could be employed in the optimisation of improved wing shapes for micro air vehicles.
${\sim}50\,\%$) than the initial rectangular wing forebear. Interestingly, the optimised shapes are found to have a large area outboard, broadly in line with the features of high-lift forewings of multi-winged insects. According to specific aerodynamic performance requirements, this novel method could be employed in the optimisation of improved wing shapes for micro air vehicles.
