Published online by Cambridge University Press: 11 November 2021
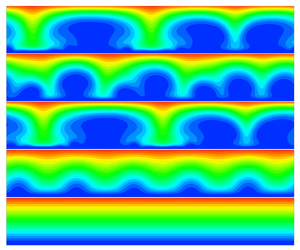
We study the effects of interfacial kinetics on the electro-hydrodynamics of ion transport near an ion-selective surface using a combination of linear stability analysis and numerical simulation. The finite kinetics of the electrolyte–electrode interface affects the ion transfer and electroconvection in many ways. On a surface of fixed topography, such as a metal surface of slow and stable ion deposition or covered by a polymer membrane, the finite kinetics reduces the current in one-dimensional ion diffusion/migration, increases the critical voltage for the onset of the electroconvective instability, changes the dynamics of the electroconvection and the overlimiting current, and enhances the lateral ion diffusion within the interfacial layer. The first three effects are indirectly caused by the reaction kinetics and can be characterized by an effective voltage difference across the liquid electrolyte. In comparison, the last effect is controlled by a direct interplay between kinetics and nonlinear electroconvection. Scaling laws for ion transport and features of electroconvection are proposed. We also analyse the linear stability of a surface which evolves under ion deposition and find that the finite kinetics decreases the growth rate of both electroconvective and morphological instabilities and therefore modifies the wavenumber of the most unstable mode.