Article contents
Electrically modulated dynamics of a compound droplet in a confined microfluidic environment
Published online by Cambridge University Press: 11 November 2019
Abstract
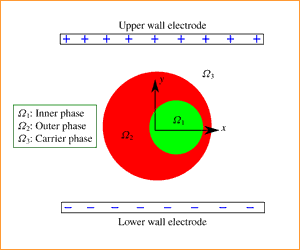
Compound droplets confined in a microfluidic channel often exhibit intriguing shapes, primarily attributable to complex hydrodynamic interactions over small scales. Here, we show that the effect of electrohydrodynamic interactions may modulate the shape evolution of the same in a somewhat non-trivial manner. By adopting a phase field formalism, our studies reveal that the combined influence of electrohydrodynamics and fluidic confinement eventually culminates towards influencing the droplet transients, distortion of the local field, as well as droplet stabilization or destabilization, allowing one to develop different regimes of shape evolution that are distinct from the ones reported in earlier studies on single droplet dynamics. Under the assumption of negligible fluid inertia and small shape deformation, we also develop an asymptotic model to predict the transient as well as the steady-state behaviour of the compound droplet for the limiting case of an unbounded suspending medium. The relative magnitude of the permittivity and conductivity of the system, in conjunction with the channel confinement, is seen to play an important role in altering the deformation characteristics of either of the interfaces. We further observe that, depending on these electrical properties, the inner droplet, if eccentrically located, may exhibit a to-and-fro or a simple translational motion. Remarkably, below a threshold confinement dimension, we unravel the onset of a definitive translational motion of the inner droplet instead of a more intuitive to-and-fro motion, thereby rendering its migration characteristics to be independent of any electrical properties. Furthermore, the viscosity contrast of the fluid phase also plays a vital role in controlling the motion and deformation dynamics of the droplet in both confined and unbounded domains. These results may bear far-reaching consequences towards understanding the control of cellular dynamics in confined in vivo physiological passages by introducing embedded electrical chips, as well as electrohydrodynamically modulated lab-on-a-chip devices for medical diagnostics on a cellular level.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 32
- Cited by

