Article contents
The elastic Landau–Levich problem on a slope
Published online by Cambridge University Press: 26 November 2019
Abstract
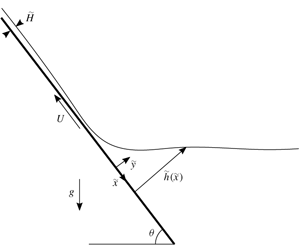
The elastic analogue of the Landau–Levich dip-coating problem, in which a plate is withdrawn from a bath of fluid on whose surface lies a thin elastic sheet, is analysed for angle of withdrawal  $\unicode[STIX]{x1D703}$ to the horizontal. The flow is controlled by the elasticity number,
$\unicode[STIX]{x1D703}$ to the horizontal. The flow is controlled by the elasticity number,  $El$, which is a measure of the relative importance of viscous and bending stresses, and
$El$, which is a measure of the relative importance of viscous and bending stresses, and  $\unicode[STIX]{x1D703}$. The leading-order solution for small
$\unicode[STIX]{x1D703}$. The leading-order solution for small  $El$ is a steady profile in which the thickness of the film on the plate is found to vary as
$El$ is a steady profile in which the thickness of the film on the plate is found to vary as  $El^{3/4}/(1-\cos \unicode[STIX]{x1D703})^{5/8}$. This prediction is confirmed in the limit
$El^{3/4}/(1-\cos \unicode[STIX]{x1D703})^{5/8}$. This prediction is confirmed in the limit  $\unicode[STIX]{x1D703}\ll 1$ by comparison with numerical simulation. Finally, the circumstances under which the assumption of a steady solution is no longer valid are discussed, and the time-dependent solution is described.
$\unicode[STIX]{x1D703}\ll 1$ by comparison with numerical simulation. Finally, the circumstances under which the assumption of a steady solution is no longer valid are discussed, and the time-dependent solution is described.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 5
- Cited by

