Article contents
Effects of kinematic and magnetic boundary conditions on the dynamics of convection-driven plane layer dynamos
Published online by Cambridge University Press: 02 November 2022
Abstract
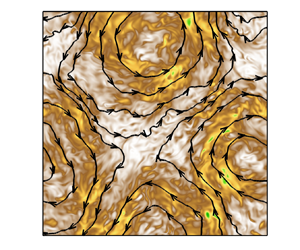
Rapidly rotating convection-driven dynamos are investigated under different kinematic and magnetic boundary conditions using direct numerical simulations. At a fixed rotation rate, represented by the Ekman number  $Ek=5\times 10^{-7}$, the thermal forcing is varied from
$Ek=5\times 10^{-7}$, the thermal forcing is varied from  $2$ to
$2$ to  $20$ times its value at the onset of convection (
$20$ times its value at the onset of convection ( $\mathcal {R}=Ra/Ra_c=2\unicode{x2013}20$, where
$\mathcal {R}=Ra/Ra_c=2\unicode{x2013}20$, where  $Ra$ is the Rayleigh number), keeping the fluid properties constant (
$Ra$ is the Rayleigh number), keeping the fluid properties constant ( $Pr=Pr_m=1$, where
$Pr=Pr_m=1$, where  $Pr$ and
$Pr$ and  $Pr_m$ are the thermal and magnetic Prandtl numbers). The statistical behaviour of the dynamos, including the force balance, energetics, and heat transport, depends on the boundary conditions that dictate both the boundary layer and the interior dynamics. At a fixed thermal forcing (
$Pr_m$ are the thermal and magnetic Prandtl numbers). The statistical behaviour of the dynamos, including the force balance, energetics, and heat transport, depends on the boundary conditions that dictate both the boundary layer and the interior dynamics. At a fixed thermal forcing ( $\mathcal {R}=3$), the structure and strength of the magnetic field produced by the dynamos, especially near the walls, depend on both velocity and magnetic boundary conditions. Though the leading-order force balance in the bulk remains geostrophic, the Lorentz force becomes comparable to the Coriolis force inside the thermal boundary layer with no-slip, perfectly conducting conditions. In this case, a term signifying the work done by the Lorentz force in the turbulent kinetic energy (TKE) equation is found to have some components that extract energy from the velocity field to produce the magnetic field, while some other components extract energy from the magnetic field to produce TKE. However, with no-slip, pseudo-vacuum conditions, all the components of the work done by the Lorentz force perform unidirectional energy transfer to produce magnetic energy from the kinetic energy of the fluid to sustain dynamo action. We find heat transfer enhancement in the rotating dynamo convection, as compared with non-magnetic rotating convection, with the peak enhancement lying in the range
$\mathcal {R}=3$), the structure and strength of the magnetic field produced by the dynamos, especially near the walls, depend on both velocity and magnetic boundary conditions. Though the leading-order force balance in the bulk remains geostrophic, the Lorentz force becomes comparable to the Coriolis force inside the thermal boundary layer with no-slip, perfectly conducting conditions. In this case, a term signifying the work done by the Lorentz force in the turbulent kinetic energy (TKE) equation is found to have some components that extract energy from the velocity field to produce the magnetic field, while some other components extract energy from the magnetic field to produce TKE. However, with no-slip, pseudo-vacuum conditions, all the components of the work done by the Lorentz force perform unidirectional energy transfer to produce magnetic energy from the kinetic energy of the fluid to sustain dynamo action. We find heat transfer enhancement in the rotating dynamo convection, as compared with non-magnetic rotating convection, with the peak enhancement lying in the range  $\mathcal {R}=3\unicode{x2013}4$. For free-slip conditions, in the absence of an Ekman layer, the dynamo action may alter the heat transport significantly by suppressing the formation of large-scale vortices. However, the highest heat transfer enhancement is found at
$\mathcal {R}=3\unicode{x2013}4$. For free-slip conditions, in the absence of an Ekman layer, the dynamo action may alter the heat transport significantly by suppressing the formation of large-scale vortices. However, the highest heat transfer enhancement is found at  $\mathcal {R}=3$ with no-slip, perfectly conducting walls, which can be attributed to a local magnetorelaxation of the rotational constraint due to enhanced Lorentz force inside the thermal boundary layer.
$\mathcal {R}=3$ with no-slip, perfectly conducting walls, which can be attributed to a local magnetorelaxation of the rotational constraint due to enhanced Lorentz force inside the thermal boundary layer.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
REFERENCES
- 7
- Cited by


