Article contents
Dynamics and structure of an apolar active suspension in an annulus
Published online by Cambridge University Press: 27 November 2017
Abstract
We study the complex dynamics of a two-dimensional suspension comprising non-motile active particles confined in an annulus. A coarse-grained liquid crystal model is employed to describe the nematic structure evolution, and is hydrodynamically coupled with the Stokes equation to solve for the induced active flows in the annulus. For dilute suspensions, coherent structures are captured by varying the particle activity and gap width, including unidirectional circulations, travelling waves and chaotic flows. For concentrated suspensions, the internal collective dynamics features motile disclination defects and flows at finite gap widths. In particular, we observe an intriguing quasi-steady-state at certain gap widths during which 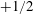 $+1/2$ -order defects oscillate around equilibrium positions accompanying travelling-wave flows that switch circulating directions periodically. We perform linear stability analyses to reveal the underlying physical mechanisms of pattern formation during a concatenation of instabilities.
$+1/2$ -order defects oscillate around equilibrium positions accompanying travelling-wave flows that switch circulating directions periodically. We perform linear stability analyses to reveal the underlying physical mechanisms of pattern formation during a concatenation of instabilities.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
Chen et al. supplementary movie 1
Supplementary movie 1: Nematic director/order (left) and flow vector/vorticity (right) for a dense Extensor suspension confined in an annulus when choosing α = -2.0, R1 = 0.75, R2 = 2.0, β = 0.874, ζ = 0.5, dT = dR = 0.025. The black scale bar represents the dimensionless length 1.0.
Chen et al. supplementary movie 2
Supplementary movie 2: Nematic director/order (left) and flow vector/vorticity (right) for a dense Extensor suspension confined in an annulus when choosing α = -2.0, R1 = 0.5, R2 = 1.6, β = 0.874, ζ = 0.5, dT = dR = 0.025. The black scale bar represents the dimensionless length 1.0.
Chen et al. supplementary movie 3
Supplementary movie 3: Nematic director/order (left) and flow vector/vorticity (right) for a dense Extensor suspension confined in an annulus when choosing α = -2.0, R1 = 0.75, R2 = 3.0, β = 0.874, ζ = 0.5, dT = dR = 0.025. The black scale bar represents the dimensionless length 1.0.
- 22
- Cited by


