Article contents
Direct numerical simulation of turbulence over systematically varied irregular rough surfaces
Published online by Cambridge University Press: 25 January 2019
Abstract
Lattice Boltzmann direct numerical simulation of turbulent open-channel flows over randomly distributed hemispheres at 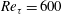 $Re_{\unicode[STIX]{x1D70F}}=600$ is carried out to reveal the influence of roughness parameters related to a probability density function of rough-surface elevation on turbulence by analysing the spatial and Reynolds- (double-) averaged Navier–Stokes equation. This study specifically concentrates on the influence of the root-mean-square roughness and the skewness, and profiles of turbulence statistics are compared by introducing an effective wall-normal distance defined as a wall-normal integrated plane porosity. The effective distance can completely collapse the total shear stress outside the roughness sublayer, and thus the similarity of the streamwise mean velocity is clearer by introducing the effective distance. In order to examine the influence of the root-mean-square roughness and the skewness on dynamical effects that contribute to an increase in the skin friction coefficient, the triple-integrated double-averaged Navier–Stokes equation is analysed. The main contributors to the skin friction coefficient are found to be turbulence and drag force. The turbulence contribution increases with the root-mean-square roughness and/or the skewness. The drag force contribution, on the other hand, increases in particular with the root-mean-square roughness whereas an increase in the skewness does not increase the drag force contribution because it does not necessarily increase the surface area of the roughness elements. The contribution of the mean velocity dispersion induced by spatial inhomogeneity of the rough surfaces substantially increases with the root-mean-square roughness. A linear correlation is confirmed between the root-mean-square roughness and the equivalent roughness while the equivalent roughness monotonically increases with the skewness. A new correlation function based on the root-mean-square roughness and the skewness is developed with the available experimental and direct numerical simulation data, and it is confirmed that the developed correlation reasonably predicts the equivalent roughness of various types of real rough surfaces.
$Re_{\unicode[STIX]{x1D70F}}=600$ is carried out to reveal the influence of roughness parameters related to a probability density function of rough-surface elevation on turbulence by analysing the spatial and Reynolds- (double-) averaged Navier–Stokes equation. This study specifically concentrates on the influence of the root-mean-square roughness and the skewness, and profiles of turbulence statistics are compared by introducing an effective wall-normal distance defined as a wall-normal integrated plane porosity. The effective distance can completely collapse the total shear stress outside the roughness sublayer, and thus the similarity of the streamwise mean velocity is clearer by introducing the effective distance. In order to examine the influence of the root-mean-square roughness and the skewness on dynamical effects that contribute to an increase in the skin friction coefficient, the triple-integrated double-averaged Navier–Stokes equation is analysed. The main contributors to the skin friction coefficient are found to be turbulence and drag force. The turbulence contribution increases with the root-mean-square roughness and/or the skewness. The drag force contribution, on the other hand, increases in particular with the root-mean-square roughness whereas an increase in the skewness does not increase the drag force contribution because it does not necessarily increase the surface area of the roughness elements. The contribution of the mean velocity dispersion induced by spatial inhomogeneity of the rough surfaces substantially increases with the root-mean-square roughness. A linear correlation is confirmed between the root-mean-square roughness and the equivalent roughness while the equivalent roughness monotonically increases with the skewness. A new correlation function based on the root-mean-square roughness and the skewness is developed with the available experimental and direct numerical simulation data, and it is confirmed that the developed correlation reasonably predicts the equivalent roughness of various types of real rough surfaces.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 52
- Cited by

