Article contents
Detonation propagation for shock-driven, subsonic and supersonic confiner flow
Published online by Cambridge University Press: 20 December 2019
Abstract
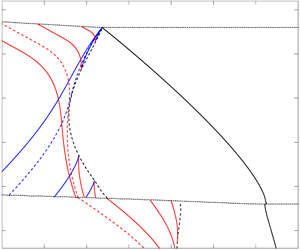
We study the compressible flow dynamics of two-dimensional, steady detonation wave propagation in a high explosive (HE) confined by aluminium (Al) or stainless steel (SS), outside of which is an air layer. We examine how the thickness of the confinement affects the subsonic detonation driving zone structure (DDZ) and the detonation speed  $(D_{0})$, demonstrating a strong dependence on whether the oblique shock-driven flow in the confiner is supersonic, as for SS, or subsonic, as for Al. A characteristic path analysis is used to examine the information flow from the material boundaries through the supersonic flow regions in both the HE and confiner that can impact the sonic surfaces bounding the subsonic flow regions. It is shown that the nature of gas-dynamic wave reflection off the SS–air or Al–air boundary can significantly influence the DDZ and
$(D_{0})$, demonstrating a strong dependence on whether the oblique shock-driven flow in the confiner is supersonic, as for SS, or subsonic, as for Al. A characteristic path analysis is used to examine the information flow from the material boundaries through the supersonic flow regions in both the HE and confiner that can impact the sonic surfaces bounding the subsonic flow regions. It is shown that the nature of gas-dynamic wave reflection off the SS–air or Al–air boundary can significantly influence the DDZ and  $D_{0}$.
$D_{0}$.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 4
- Cited by

