Article contents
Decoupling ablation effects on boundary-layer stability and transition
Published online by Cambridge University Press: 20 November 2020
Abstract
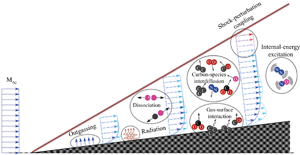
A modelling methodology is proposed and applied to effectively decouple many of the multiple physical phenomena simultaneously coexisting in boundary-layer-transition problems in the presence of an ablating thermal protection system. Investigations are based on linear stability theory and the semi-empirical  $\textrm {e}^{\textrm {N}}$ method, and study the marginal contribution to second-mode-wave amplitudes of internal-energy-mode excitation, ablation-induced outgassing, ablation- and radiation-induced surface cooling, air- and carbon-species dissociation reactions, the interdiffusion of dissimilar species, surface chemistry and radiation and perturbation–shock interactions. The contributions of these phenomena are isolated by deploying a variety of flow assumptions, mixtures and boundary conditions with marginal increases in modelling complexity and generality. Internal-energy-mode excitation is seen to be the major contributor to the perturbation amplitudes for most conditions considered, whereas ablation-induced outgassing or the ablation- and radiation-induced modification of the surface-temperature distribution display a minor effect. Other phenomena are seen to have a variable contribution depending on the trajectory point, owing to the different ablation rates with which the thermal protection system decomposes. This is the case with the diffusion of carbon species injected through the surface, and the dissociation of air and carbon species. The use of a radiative equilibrium, rather than a homogeneous boundary condition on the temperature perturbation amplitude, is seen to increase the predicted growth of second-mode waves at all the trajectory points. Perturbation–shock interactions remarkably modify instability development only in scenarios with significant unstable supersonic modes. The substitution of all ablation subproducts for a single non-reacting species (
$\textrm {e}^{\textrm {N}}$ method, and study the marginal contribution to second-mode-wave amplitudes of internal-energy-mode excitation, ablation-induced outgassing, ablation- and radiation-induced surface cooling, air- and carbon-species dissociation reactions, the interdiffusion of dissimilar species, surface chemistry and radiation and perturbation–shock interactions. The contributions of these phenomena are isolated by deploying a variety of flow assumptions, mixtures and boundary conditions with marginal increases in modelling complexity and generality. Internal-energy-mode excitation is seen to be the major contributor to the perturbation amplitudes for most conditions considered, whereas ablation-induced outgassing or the ablation- and radiation-induced modification of the surface-temperature distribution display a minor effect. Other phenomena are seen to have a variable contribution depending on the trajectory point, owing to the different ablation rates with which the thermal protection system decomposes. This is the case with the diffusion of carbon species injected through the surface, and the dissociation of air and carbon species. The use of a radiative equilibrium, rather than a homogeneous boundary condition on the temperature perturbation amplitude, is seen to increase the predicted growth of second-mode waves at all the trajectory points. Perturbation–shock interactions remarkably modify instability development only in scenarios with significant unstable supersonic modes. The substitution of all ablation subproducts for a single non-reacting species ( $\textrm {CO}_{2}$) was acceptable as long as the flow chemistry can be assumed frozen. The use of inaccurate transport and diffusion models, rather than the state of the art, is seen to have a variable effect on the predictions, yet generally smaller than what was observed in previous work.
$\textrm {CO}_{2}$) was acceptable as long as the flow chemistry can be assumed frozen. The use of inaccurate transport and diffusion models, rather than the state of the art, is seen to have a variable effect on the predictions, yet generally smaller than what was observed in previous work.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
REFERENCES
- 7
- Cited by


