Article contents
Control of oblique breakdown in a supersonic boundary layer employing a local cooling strip
Published online by Cambridge University Press: 23 September 2022
Abstract
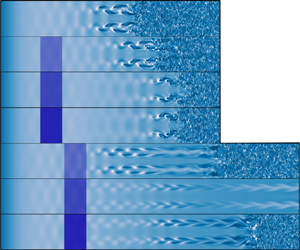
Oblique breakdown in a Mach 2.0 supersonic boundary layer controlled by a local cooling strip with a temperature jump is investigated using direct numerical simulations and linear stability theory. The effect of temperature on the stability of the fundamental oblique waves is first studied by linear stability theory. It is shown that the growth rate of fundamental oblique waves will decrease monotonically as the temperature decreases. However, the results of the direct numerical simulations indicate that transition reversal will occur as the growth rate of the fundamental oblique waves of cooled case becomes faster compared with that of baseline case downstream of the cooling strip. When the cooling strip is in the linear region, the transition is delayed due to the suppression effect of the cooling strip on the fundamental oblique waves. When the cooling strip is located in the early nonlinear region, the fundamental oblique waves will be suppressed by higher spanwise wavenumber steady modes generated by the mutual and self-interaction between the fundamental oblique waves and harmonic modes, which is first called the self-suppression effect (SSE) in the present study. Further research indicated that the meanflow distortion generated by steady modes plays an important role in the SSE. Compared with the stabilization effect of the cooling strip, the SSE is more effective. Moreover, the SSE might provide a new idea on the instability control, as it is observed that the SSE works three times leading to the growth rate of fundamental oblique waves slowing down at three different regions, respectively.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
REFERENCES
- 11
- Cited by


