Article contents
Computations of equilibrium and non-equilibrium turbulent channel flows using a nested-LES approach
Published online by Cambridge University Press: 22 March 2016
Abstract
A new nested-LES approach for computation of high Reynolds number, equilibrium, and non-equilibrium, wall-bounded turbulent flows is presented. The method couples coarse-resolution LES in the full computational domain with fine-resolution LES in a minimal flow unit to retain the accuracy of well-resolved LES throughout the computational domain, including in the near-wall region, while significantly reducing the computational cost. The two domains are coupled by renormalizing the instantaneous velocity fields in each domain dynamically during the course of the simulation to match the wall-normal profiles of single-time, ensemble-averaged kinetic energies of the components of ‘mean’ and fluctuating velocities in the inner layer to those of the minimal flow unit, and in the outer layer to those of the full domain. This simple renormalization procedure is shown to correct the energy spectra and wall shear stresses in both domains, thus leading to accurate turbulence statistics. The nested-LES approach has been applied to computation of equilibrium turbulent channel flow at 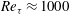 $Re_{{\it\tau}}\approx 1000$ , 2000, 5000, 10 000, and non-equilibrium, strained turbulent channel flow at
$Re_{{\it\tau}}\approx 1000$ , 2000, 5000, 10 000, and non-equilibrium, strained turbulent channel flow at 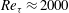 $Re_{{\it\tau}}\approx 2000$ . In both flows, nested-LES predicts the skin friction coefficient, first- and higher-order turbulence statistics, spectra and structure of the flow in agreement with available DNS and experimental data. Nested-LES can be applied to any flow with at least one direction of local or global homogeneity, while reducing the required number of grid points from
$Re_{{\it\tau}}\approx 2000$ . In both flows, nested-LES predicts the skin friction coefficient, first- and higher-order turbulence statistics, spectra and structure of the flow in agreement with available DNS and experimental data. Nested-LES can be applied to any flow with at least one direction of local or global homogeneity, while reducing the required number of grid points from 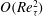 $O(Re_{{\it\tau}}^{2})$ of conventional LES to
$O(Re_{{\it\tau}}^{2})$ of conventional LES to 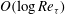 $O(\log Re_{{\it\tau}})$ or
$O(\log Re_{{\it\tau}})$ or 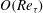 $O(Re_{{\it\tau}})$ in flows with two or one locally or globally homogeneous directions, respectively.
$O(Re_{{\it\tau}})$ in flows with two or one locally or globally homogeneous directions, respectively.
Information
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 8
- Cited by


