Article contents
A comparative study of the velocity and vorticity structure in pipes and boundary layers at friction Reynolds numbers up to 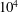 $10^{4}$
$10^{4}$
Published online by Cambridge University Press: 23 April 2019
Abstract
This study presents findings from a first-of-its-kind measurement campaign that includes simultaneous measurements of the full velocity and vorticity vectors in both pipe and boundary layer flows under matched spatial resolution and Reynolds number conditions. Comparison of canonical turbulent flows offers insight into the role(s) played by features that are unique to one or the other. Pipe and zero pressure gradient boundary layer flows are often compared with the goal of elucidating the roles of geometry and a free boundary condition on turbulent wall flows. Prior experimental efforts towards this end have focused primarily on the streamwise component of velocity, while direct numerical simulations are at relatively low Reynolds numbers. In contrast, this study presents experimental measurements of all three components of both velocity and vorticity for friction Reynolds numbers 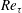 $Re_{\unicode[STIX]{x1D70F}}$ ranging from 5000 to 10 000. Differences in the two transverse Reynolds normal stresses are shown to exist throughout the log layer and wake layer at Reynolds numbers that exceed those of existing numerical data sets. The turbulence enstrophy profiles are also shown to exhibit differences spanning from the outer edge of the log layer to the outer flow boundary. Skewness and kurtosis profiles of the velocity and vorticity components imply the existence of a ‘quiescent core’ in pipe flow, as described by Kwon et al. (J. Fluid Mech., vol. 751, 2014, pp. 228–254) for channel flow at lower
$Re_{\unicode[STIX]{x1D70F}}$ ranging from 5000 to 10 000. Differences in the two transverse Reynolds normal stresses are shown to exist throughout the log layer and wake layer at Reynolds numbers that exceed those of existing numerical data sets. The turbulence enstrophy profiles are also shown to exhibit differences spanning from the outer edge of the log layer to the outer flow boundary. Skewness and kurtosis profiles of the velocity and vorticity components imply the existence of a ‘quiescent core’ in pipe flow, as described by Kwon et al. (J. Fluid Mech., vol. 751, 2014, pp. 228–254) for channel flow at lower 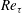 $Re_{\unicode[STIX]{x1D70F}}$, and characterize the extent of its influence in the pipe. Observed differences between statistical profiles of velocity and vorticity are then discussed in the context of a structural difference between free-stream intermittency in the boundary layer and ‘quiescent core’ intermittency in the pipe that is detectable to wall distances as small as 5 % of the layer thickness.
$Re_{\unicode[STIX]{x1D70F}}$, and characterize the extent of its influence in the pipe. Observed differences between statistical profiles of velocity and vorticity are then discussed in the context of a structural difference between free-stream intermittency in the boundary layer and ‘quiescent core’ intermittency in the pipe that is detectable to wall distances as small as 5 % of the layer thickness.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 17
- Cited by

