Published online by Cambridge University Press: 27 September 2012
This paper focuses on turbulence structure in a fully developed rough-wall channel flow and its role in subgrid-scale (SGS) energy transfer. Our previous work has shown that eddies of scale comparable to the roughness elements are generated near the wall, and are lifted up rapidly by large-scale coherent structures to flood the flow field well above the roughness sublayer. Utilizing high-resolution and time-resolved particle-image-velocimetry datasets obtained in an optically index-matched facility, we decompose the turbulence into large (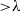 ${\gt }\lambda $), intermediate (
${\gt }\lambda $), intermediate (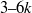 $3\text{{\ndash}} 6k$), roughness (
$3\text{{\ndash}} 6k$), roughness ( $1\text{{\ndash}} 3k$) and small (
$1\text{{\ndash}} 3k$) and small (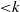 ${\lt }k$) scales, where
${\lt }k$) scales, where 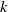 $k$ and
$k$ and 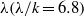 $\lambda (\lambda / k= 6. 8)$ are roughness height and wavelength, respectively. With decreasing distance from the wall, there is a marked increase in the ‘non-local’ SGS energy flux directly from large to small scales and in the fraction of turbulence dissipated by roughness-scale eddies. Conditional averaging is used to show that a small fraction of the flow volume (e.g. 5 %), which contains the most intense SGS energy transfer events, is responsible for a substantial fraction (50 %) of the energy flux from resolved to subgrid scales. In streamwise wall-normal (
$\lambda (\lambda / k= 6. 8)$ are roughness height and wavelength, respectively. With decreasing distance from the wall, there is a marked increase in the ‘non-local’ SGS energy flux directly from large to small scales and in the fraction of turbulence dissipated by roughness-scale eddies. Conditional averaging is used to show that a small fraction of the flow volume (e.g. 5 %), which contains the most intense SGS energy transfer events, is responsible for a substantial fraction (50 %) of the energy flux from resolved to subgrid scales. In streamwise wall-normal (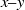 $x\text{{\ndash}} y$) planes, the averaged flow structure conditioned on high SGS energy flux exhibits a large inclined shear layer containing negative vorticity, bounded by an ejection below and a sweep above. Near the wall the sweep is dominant, while in the outer layer the ejection is stronger. The peaks of SGS flux and kinetic energy within the inclined layer are spatially displaced from the region of high resolved turbulent kinetic energy. Accordingly, some of the highest correlations occur between spatially displaced resolved velocity gradients and SGS stresses. In wall-parallel
$x\text{{\ndash}} y$) planes, the averaged flow structure conditioned on high SGS energy flux exhibits a large inclined shear layer containing negative vorticity, bounded by an ejection below and a sweep above. Near the wall the sweep is dominant, while in the outer layer the ejection is stronger. The peaks of SGS flux and kinetic energy within the inclined layer are spatially displaced from the region of high resolved turbulent kinetic energy. Accordingly, some of the highest correlations occur between spatially displaced resolved velocity gradients and SGS stresses. In wall-parallel 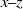 $x\text{{\ndash}} z$ planes, the conditional flow field exhibits two pairs of counter-rotating vortices that induce a contracting flow at the peak of SGS flux. Instantaneous realizations in the roughness sublayer show the presence of the counter-rotating vortex pairs at the intersection of two vortex trains, each containing multiple
$x\text{{\ndash}} z$ planes, the conditional flow field exhibits two pairs of counter-rotating vortices that induce a contracting flow at the peak of SGS flux. Instantaneous realizations in the roughness sublayer show the presence of the counter-rotating vortex pairs at the intersection of two vortex trains, each containing multiple 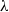 $\lambda $-spaced vortices of the same sign. In the outer layer, the SGS flux peaks within isolated vortex trains that retain the roughness signature, and the distinct pattern of two counter-rotating vortex pairs disappears. To explain the planar signatures, we propose a flow consisting of U-shaped quasi-streamwise vortices that develop as spanwise vorticity is stretched in regions of high streamwise velocity between roughness elements. Flow induced by adjacent legs of the U-shaped structures causes powerful ejections, which lift these vortices away from the wall. As a sweep is transported downstream, its interaction with the roughness generates a series of such events, leading to the formation of inclined vortex trains.
$\lambda $-spaced vortices of the same sign. In the outer layer, the SGS flux peaks within isolated vortex trains that retain the roughness signature, and the distinct pattern of two counter-rotating vortex pairs disappears. To explain the planar signatures, we propose a flow consisting of U-shaped quasi-streamwise vortices that develop as spanwise vorticity is stretched in regions of high streamwise velocity between roughness elements. Flow induced by adjacent legs of the U-shaped structures causes powerful ejections, which lift these vortices away from the wall. As a sweep is transported downstream, its interaction with the roughness generates a series of such events, leading to the formation of inclined vortex trains.