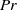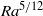Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Whitehead, Jared P.
and
Wittenberg, Ralf W.
2014.
A rigorous bound on the vertical transport of heat in Rayleigh-Bénard convection at infinite Prandtl number with mixed thermal boundary conditions.
Journal of Mathematical Physics,
Vol. 55,
Issue. 9,
Goluskin, David
and
Doering, Charles R.
2016.
Bounds for convection between rough boundaries.
Journal of Fluid Mechanics,
Vol. 804,
Issue. ,
p.
370.
Fei, Mingwen
Han, Daozhi
and
Wang, Xiaoming
2017.
Initial–boundary layer associated with the nonlinear Darcy–Brinkman–Oberbeck–Boussinesq system.
Physica D: Nonlinear Phenomena,
Vol. 338,
Issue. ,
p.
42.
Doering, Charles R.
Wu, Jiahong
Zhao, Kun
and
Zheng, Xiaoming
2018.
Long time behavior of the two-dimensional Boussinesq equations without buoyancy diffusion.
Physica D: Nonlinear Phenomena,
Vol. 376-377,
Issue. ,
p.
144.
Tao, Lizheng
Wu, Jiahong
Zhao, Kun
and
Zheng, Xiaoming
2020.
Stability Near Hydrostatic Equilibrium to the 2D Boussinesq Equations Without Thermal Diffusion.
Archive for Rational Mechanics and Analysis,
Vol. 237,
Issue. 2,
p.
585.
Cao, Chongsheng
Guo, Yanqiu
and
Titi, Edriss S.
2021.
Global well-posedness for a rapidly rotating convection model of tall columnar structure in the limit of infinite Prandtl number.
Journal of Evolution Equations,
Vol. 21,
Issue. 3,
p.
2923.
Nobili, Camilla
2022.
The role of boundary conditions in scaling laws for turbulent heat transport.
Mathematics in Engineering,
Vol. 5,
Issue. 1,
p.
1.
Drivas, Theodore D.
Nguyen, Huy Q.
and
Nobili, Camilla
2022.
Bounds on heat flux for Rayleigh–Bénard convection between Navier-slip fixed-temperature boundaries.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 380,
Issue. 2225,
Bleitner, F.
and
Nobili, C.
2024.
Scaling laws for Rayleigh–Bénard convection between Navier-slip boundaries.
Journal of Fluid Mechanics,
Vol. 998,
Issue. ,
Arslan, Ali
2024.
Internally heated convection with rotation: bounds on heat transport.
Journal of Fluid Mechanics,
Vol. 1001,
Issue. ,
Arslan, Ali
and
Rojas, Rubén E.
2025.
New bounds for heat transport in internally heated convection at infinite Prandtl number.
Journal of Mathematical Physics,
Vol. 66,
Issue. 2,