Article contents
Bistability of the large-scale dynamics in quasi-two-dimensional turbulence
Published online by Cambridge University Press: 24 March 2022
Abstract
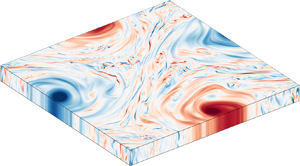
In many geophysical and astrophysical flows, suppression of fluctuations along one direction of the flow drives a quasi-two-dimensional upscale flux of kinetic energy, leading to the formation of strong vortex condensates at the largest scales. Recent studies have shown that the transition towards this condensate state is hysteretic, giving rise to a limited bistable range in which both the condensate state as well as the regular three-dimensional state can exist at the same parameter values. In this work, we use direct numerical simulations of thin-layer flow to investigate whether this bistable range survives as the domain size and turbulence intensity are increased. By studying the time scales at which rare transitions occur from one state into the other, we find that the bistable range grows as the box size and/or Reynolds number  $Re$ are increased, showing that the bistability is neither a finite-size nor a finite-
$Re$ are increased, showing that the bistability is neither a finite-size nor a finite- $Re$ effect. We furthermore predict a cross-over from a bimodal regime at low box size, low
$Re$ effect. We furthermore predict a cross-over from a bimodal regime at low box size, low  $Re$ to a regime of pure hysteresis at high box size, high
$Re$ to a regime of pure hysteresis at high box size, high  $Re$, in which any transition from one state to the other is prohibited at any finite time scale.
$Re$, in which any transition from one state to the other is prohibited at any finite time scale.
JFM classification
Information
- Type
- JFM Rapids
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
REFERENCES
- 14
- Cited by


