Article contents
Azimuthal capillary waves on a hollow filament – the discrete and the continuous spectrum
Published online by Cambridge University Press: 25 November 2019
Abstract
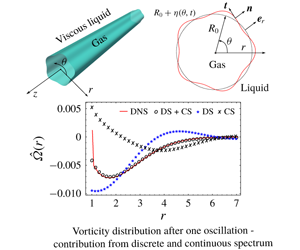
We study the temporal spectrum of linearised, azimuthal, interfacial perturbations imposed on a cylindrical gaseous filament surrounded by immiscible, viscous, quiescent fluid in radially unbounded geometry. Linear stability analysis shows that the base state is stable to azimuthal perturbations of standing wave form. Normal mode analysis leads to a viscous dispersion relation and shows that in addition to the discrete spectrum, the problem also admits a continuous spectrum. For a given azimuthal Fourier mode and Laplace number, the discrete spectrum yields two eigenfunctions which decay exponentially to zero at large radii and thus cannot represent far field perturbations. In addition to these discrete modes, we find an uncountably infinite set of eigenmodes which decay algebraically to zero. The completeness theorem for perturbation vorticity may be expressed as a sum over the discrete modes and an integral over the continuous ones. We validate our normal mode results by solving the linearised, initial value problem (IVP). The initial perturbation is taken to be an interfacial, azimuthal Fourier mode with zero perturbation vorticity. It is shown that the expression for the time dependent amplitude of a capillary standing wave (in the Laplace domain,  $s$) has poles and branch points on the complex
$s$) has poles and branch points on the complex  $s$ plane. We show that the residue at the poles yields the discrete spectrum, while the contribution from either side of the branch cut provides the continuous spectrum contribution. The particular initial condition treated here in the IVP, has projections on the discrete as well as the continuous spectrum eigenmodes and thus both sets are excited initially. Consequently the time evolution of the standing wave amplitude and the perturbation vorticity field have the form of a sum over discrete exponential contributions and an integral over a continuous range of exponential terms. The solution to the IVP leads to explicit analytical expressions for the standing wave amplitude and the vorticity field in the fluid outside the filament. Linearised analytical results are validated using direct numerical simulations (DNS) conducted using a code developed in-house for solving the incompressible, Navier–Stokes equations with an interface. For small perturbation amplitude, analytical predictions show excellent agreement with DNS. Our analysis complements and extends earlier results on the discrete and the continuous spectrum for interfacial viscous, capillary waves on unbounded domain.
$s$ plane. We show that the residue at the poles yields the discrete spectrum, while the contribution from either side of the branch cut provides the continuous spectrum contribution. The particular initial condition treated here in the IVP, has projections on the discrete as well as the continuous spectrum eigenmodes and thus both sets are excited initially. Consequently the time evolution of the standing wave amplitude and the perturbation vorticity field have the form of a sum over discrete exponential contributions and an integral over a continuous range of exponential terms. The solution to the IVP leads to explicit analytical expressions for the standing wave amplitude and the vorticity field in the fluid outside the filament. Linearised analytical results are validated using direct numerical simulations (DNS) conducted using a code developed in-house for solving the incompressible, Navier–Stokes equations with an interface. For small perturbation amplitude, analytical predictions show excellent agreement with DNS. Our analysis complements and extends earlier results on the discrete and the continuous spectrum for interfacial viscous, capillary waves on unbounded domain.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 4
- Cited by

