Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Talluru, K. M.
Philip, J.
and
Chauhan, K. A.
2018.
Local transport of passive scalar released from a point source in a turbulent boundary layer.
Journal of Fluid Mechanics,
Vol. 846,
Issue. ,
p.
292.
Chin, Rey C.
and
Philip, Jimmy
2019.
Direct numerical simulation of low Reynolds number turbulent swirling pipe flows.
Physical Review Fluids,
Vol. 4,
Issue. 11,
Cantwell, Brian J.
2019.
A universal velocity profile for smooth wall pipe flow.
Journal of Fluid Mechanics,
Vol. 878,
Issue. ,
p.
834.
Baidya, R.
Baars, W. J.
Zimmerman, S.
Samie, M.
Hearst, R. J.
Dogan, E.
Mascotelli, L.
Zheng, X.
Bellani, G.
Talamelli, A.
Ganapathisubramani, B.
Hutchins, N.
Marusic, I.
Klewicki, J.
and
Monty, J. P.
2019.
Simultaneous skin friction and velocity measurements in high Reynolds number pipe and boundary layer flows.
Journal of Fluid Mechanics,
Vol. 871,
Issue. ,
p.
377.
Bautista, Juan Carlos Cuevas
Ebadi, Alireza
White, Christopher M.
Chini, Gregory P.
and
Klewicki, Joseph C.
2019.
A uniform momentum zone–vortical fissure model of the turbulent boundary layer.
Journal of Fluid Mechanics,
Vol. 858,
Issue. ,
p.
609.
Talluru, K. M.
Philip, Jimmy
and
Chauhan, K. A.
2019.
Self-similar spectra of point-source scalar plumes in a turbulent boundary layer.
Journal of Fluid Mechanics,
Vol. 870,
Issue. ,
p.
698.
Baars, Woutijn J.
and
Marusic, Ivan
2020.
Data-driven decomposition of the streamwise turbulence kinetic energy in boundary layers. Part 2. Integrated energy and .
Journal of Fluid Mechanics,
Vol. 882,
Issue. ,
George, Nitheesh
Ooi, Andrew
and
Philip, Jimmy
2021.
Evolution of a wall-attached buoyant plume in confined boxes: Direct numerical simulations, entrainment coefficient and an integral model.
International Journal of Heat and Fluid Flow,
Vol. 90,
Issue. ,
p.
108824.
Chin, Rey C.
and
Philip, Jimmy
2021.
Swirling turbulent pipe flows: Inertial region and velocity–vorticity correlations.
International Journal of Heat and Fluid Flow,
Vol. 87,
Issue. ,
p.
108767.
Perven, Rina
Philip, Jimmy
and
Klewicki, Joseph
2021.
Statistical properties of streamline geometry in turbulent wall-flows.
Physical Review Fluids,
Vol. 6,
Issue. 3,
Klewicki, J.C.
2021.
Properties of turbulent channel flow similarity solutions.
Journal of Fluid Mechanics,
Vol. 915,
Issue. ,
Baidya, R.
Philip, J.
Hutchins, N.
Monty, J.P.
and
Marusic, I.
2021.
Spanwise velocity statistics in high-Reynolds-number turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 913,
Issue. ,
Blackburn, Hugh M.
Deguchi, Kengo
and
Hall, Philip
2021.
Distributed vortex-wave interactions: the relation of self-similarity to the attached eddy hypothesis.
Journal of Fluid Mechanics,
Vol. 924,
Issue. ,
Romero, Sylvia
Zimmerman, Spencer
Philip, Jimmy
White, Christopher
and
Klewicki, Joseph
2022.
Properties of the inertial sublayer in adverse pressure-gradient turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 937,
Issue. ,
Romero, Sylvia
Zimmerman, Spencer
Philip, Jimmy
and
Klewicki, Joseph
2023.
Velocity spectra and scale decomposition of adverse pressure gradient turbulent boundary layers considering history effects.
International Journal of Heat and Fluid Flow,
Vol. 102,
Issue. ,
p.
109143.
Kramer, Matthias
and
Valero, Daniel
2023.
Linking turbulent waves and bubble diffusion in self-aerated open-channel flows: two-state air concentration.
Journal of Fluid Mechanics,
Vol. 966,
Issue. ,
Morse, Nicholas
and
Mahesh, Krishnan
2023.
Tripping effects on model-scale studies of flow over the DARPA SUBOFF.
Journal of Fluid Mechanics,
Vol. 975,
Issue. ,
Chen, Peng E.S.
Wu, Wen
Griffin, Kevin P.
Shi, Yipeng
and
Yang, Xiang I.A.
2023.
A universal velocity transformation for boundary layers with pressure gradients.
Journal of Fluid Mechanics,
Vol. 970,
Issue. ,
Lu, Yuhui
Xiang, Tianrui
Zaki, Tamer A.
and
Katz, Joseph
2024.
On the scaling and critical layer in a turbulent boundary layer over a compliant surface.
Journal of Fluid Mechanics,
Vol. 980,
Issue. ,
Romero, S.
Zimmerman, S.
Philip, J.
and
Klewicki, J.
2024.
Progress in Turbulence X.
Vol. 404,
Issue. ,
p.
83.
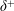 $\unicode[STIX]{x1D6FF}^{+}$ . For canonical boundary layers, the mean inertia, which is a function of the wall-normal distance, appears instead of the constant mean pressure gradient force in the MMB for pipes and channels. The constancy of the pressure gradient has led to theoretical treatments for pipes/channels, that are more precise than for the TBL. Elements of these analyses include the logarithmic behaviour of the mean velocity, specification of the Reynolds shear stress peak location, the square-root Reynolds number scaling for the log layer onset and a well-defined layer structure based on the balance of terms in the MMB. The present analyses evidence that similarly well-founded results also hold for turbulent boundary layers. This follows from transforming the mean inertia term in the MMB into a form that resembles that in pipes/channels, and is constant across the outer inertial region of the TBL. The physical reasoning is that the mean inertia is primarily a large-scale outer layer contribution, the ‘shape’ of which becomes invariant of
$\unicode[STIX]{x1D6FF}^{+}$ . For canonical boundary layers, the mean inertia, which is a function of the wall-normal distance, appears instead of the constant mean pressure gradient force in the MMB for pipes and channels. The constancy of the pressure gradient has led to theoretical treatments for pipes/channels, that are more precise than for the TBL. Elements of these analyses include the logarithmic behaviour of the mean velocity, specification of the Reynolds shear stress peak location, the square-root Reynolds number scaling for the log layer onset and a well-defined layer structure based on the balance of terms in the MMB. The present analyses evidence that similarly well-founded results also hold for turbulent boundary layers. This follows from transforming the mean inertia term in the MMB into a form that resembles that in pipes/channels, and is constant across the outer inertial region of the TBL. The physical reasoning is that the mean inertia is primarily a large-scale outer layer contribution, the ‘shape’ of which becomes invariant of 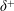 $\unicode[STIX]{x1D6FF}^{+}$ with increasing
$\unicode[STIX]{x1D6FF}^{+}$ with increasing 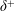 $\unicode[STIX]{x1D6FF}^{+}$ , and with a ‘magnitude’ that is inversely proportional to
$\unicode[STIX]{x1D6FF}^{+}$ , and with a ‘magnitude’ that is inversely proportional to 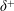 $\unicode[STIX]{x1D6FF}^{+}$ . The present analyses are enabled and corroborated using recent high resolution, large Reynolds number hot-wire measurements of all the terms in the TBL MMB.
$\unicode[STIX]{x1D6FF}^{+}$ . The present analyses are enabled and corroborated using recent high resolution, large Reynolds number hot-wire measurements of all the terms in the TBL MMB.

