Article contents
Ageostrophic instability in rotating shallow water
Published online by Cambridge University Press: 28 September 2012
Abstract
Linear instabilities, both momentum-balanced and unbalanced, in several different 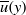 $ \overline{u} (y)$ shear profiles are investigated in the rotating shallow water equations. The unbalanced instabilities are strongly ageostrophic and involve inertia–gravity wave motions, occurring only for finite Rossby (
$ \overline{u} (y)$ shear profiles are investigated in the rotating shallow water equations. The unbalanced instabilities are strongly ageostrophic and involve inertia–gravity wave motions, occurring only for finite Rossby ( 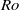 $\mathit{Ro}$ ) and Froude (
$\mathit{Ro}$ ) and Froude ( 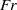 $\mathit{Fr}$ ) numbers. They serve as a possible route for the breakdown of balance in a rotating shallow water system, which leads the energy to cascade towards small scales. Unlike previous work, this paper focuses on general shear flows with non-uniform potential vorticity, and without side or equatorial boundaries or vanishing layer depth (frontal outcropping). As well as classical shear instability among balanced shear wave modes (i.e. B–B type), two types of ageostrophic instability (B–G and G–G) are found. The B–G instability has attributes of both a balanced shear wave mode and an inertia–gravity wave mode. The G–G instability occurs as a sharp resonance between two inertia–gravity wave modes. The criterion for the occurrence of the ageostrophic instability is associated with the second stability condition of Ripa (1983), which requires a sufficiently large local Froude number. When
$\mathit{Fr}$ ) numbers. They serve as a possible route for the breakdown of balance in a rotating shallow water system, which leads the energy to cascade towards small scales. Unlike previous work, this paper focuses on general shear flows with non-uniform potential vorticity, and without side or equatorial boundaries or vanishing layer depth (frontal outcropping). As well as classical shear instability among balanced shear wave modes (i.e. B–B type), two types of ageostrophic instability (B–G and G–G) are found. The B–G instability has attributes of both a balanced shear wave mode and an inertia–gravity wave mode. The G–G instability occurs as a sharp resonance between two inertia–gravity wave modes. The criterion for the occurrence of the ageostrophic instability is associated with the second stability condition of Ripa (1983), which requires a sufficiently large local Froude number. When 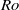 $\mathit{Ro}$ and especially
$\mathit{Ro}$ and especially 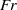 $\mathit{Fr}$ increase, the balanced instability is suppressed, while the ageostrophic instabilities are enhanced. The profile of the mean flow also affects the strength of the balanced and ageostrophic instabilities.
$\mathit{Fr}$ increase, the balanced instability is suppressed, while the ageostrophic instabilities are enhanced. The profile of the mean flow also affects the strength of the balanced and ageostrophic instabilities.
Information
- Type
- Papers
- Information
- Copyright
- ©2012 Cambridge University Press
References
- 4
- Cited by

