Article contents
Why Naive 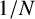 $ 1/N $ Diversification Is Not So Naive, and How to Beat It?
$ 1/N $ Diversification Is Not So Naive, and How to Beat It?
Published online by Cambridge University Press: 16 October 2023
Abstract
We show theoretically that the usual estimated investment strategies will not achieve the optimal Sharpe ratio when the dimensionality is high relative to sample size, and the 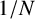 $ 1/N $ rule is optimal in a 1-factor model with diversifiable risks as dimensionality increases, which explains why it is difficult to beat the
$ 1/N $ rule is optimal in a 1-factor model with diversifiable risks as dimensionality increases, which explains why it is difficult to beat the 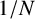 $ 1/N $ rule in practice. We also explore conditions under which it can be beaten, and find that we can outperform it by combining it with the estimated rules when
$ 1/N $ rule in practice. We also explore conditions under which it can be beaten, and find that we can outperform it by combining it with the estimated rules when  $ N $ is small, and by combining it with anomalies or machine learning portfolios, conditional on the profitability of the latter, when
$ N $ is small, and by combining it with anomalies or machine learning portfolios, conditional on the profitability of the latter, when 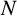 $ N $ is large.
$ N $ is large.
Information
- Type
- Research Article
- Information
- Journal of Financial and Quantitative Analysis , Volume 59 , Issue 8 , December 2024 , pp. 3601 - 3632
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of the Michael G. Foster School of Business, University of Washington
Footnotes
We are extremely grateful to two anonymous referees and Thierry Foucault (the editor) for their very detailed and insightful comments that have helped to improve the paper enormously. We are also grateful to Victor DeMiguel, John Dooley, Lorenzo Garlappi, Raymond Kan, Nathan Lassance,  $ \overset{\smile }{\mathrm{L}} $uboš Pástor, Christopher Reilly, Landon Ross, Jun Tu, Raman Uppal, Xiaolu Wang, Alex Weissensteiner, Michael Wolf, Paolo Zaffaroni, Yingguang Zhang, Ge Zhe, and seminar and conference participants at Capital University of Economics and Business, Boston College, Fudan University, Louisiana State University, Peking University, University of Manitoba, University of Nottingham, Washington University in St. Louis, the 2021 International Conference on Computational and Financial Econometrics, and 2022 China International Conference for very helpful comments. Yuan was supported in part by the Columbia-CityU/HK collaborative project that is supported by the InnoHK Initiative, The Government of the HKSAR, and the AIFT Lab. We thank Songrun He for outstanding research assistance.
$ \overset{\smile }{\mathrm{L}} $uboš Pástor, Christopher Reilly, Landon Ross, Jun Tu, Raman Uppal, Xiaolu Wang, Alex Weissensteiner, Michael Wolf, Paolo Zaffaroni, Yingguang Zhang, Ge Zhe, and seminar and conference participants at Capital University of Economics and Business, Boston College, Fudan University, Louisiana State University, Peking University, University of Manitoba, University of Nottingham, Washington University in St. Louis, the 2021 International Conference on Computational and Financial Econometrics, and 2022 China International Conference for very helpful comments. Yuan was supported in part by the Columbia-CityU/HK collaborative project that is supported by the InnoHK Initiative, The Government of the HKSAR, and the AIFT Lab. We thank Songrun He for outstanding research assistance.
References
- 10
- Cited by

