Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tong, H.
Thanoon, B.
and
Gudmundsson, G.
1985.
THRESHOLD TIME SERIES MODELING OF TWO ICELANDIC RIVERFLOW SYSTEMS1.
JAWRA Journal of the American Water Resources Association,
Vol. 21,
Issue. 4,
p.
651.
Chan, K. S.
and
Tong, H.
1985.
On the use of the deterministic Lyapunov function for the ergodicity of stochastic difference equations.
Advances in Applied Probability,
Vol. 17,
Issue. 3,
p.
666.
Petruccelli, Joseph D.
1986.
ON THE CONSISTENCY OF LEAST SQUARES ESTIMATORS FOR A THRESHOLD AR(1) MODEL.
Journal of Time Series Analysis,
Vol. 7,
Issue. 4,
p.
269.
Chan, K. S.
and
Tong, H.
1986.
A note on certain integral equations associated with non-linear time series analysis.
Probability Theory and Related Fields,
Vol. 73,
Issue. 1,
p.
153.
Chan, K. S.
and
Tong, H.
1986.
ON ESTIMATING THRESHOLDS IN AUTOREGRESSIVE MODELS.
Journal of Time Series Analysis,
Vol. 7,
Issue. 3,
p.
179.
Anděl, Jiři
and
Bartoň, Tomáŝ
1986.
A NOTE ON THE THRESHOLD AR(1) MODEL WITH CAUCHY INNOVATIONS.
Journal of Time Series Analysis,
Vol. 7,
Issue. 1,
p.
1.
Petruccelli, J. D.
and
Woolford, S. W.
1987.
On a class of threshold AR(k) processes.
Annals of Operations Research,
Vol. 9,
Issue. 1,
p.
421.
Cipra, Tomáš
1988.
Autoregressive processes in optimization.
Journal of Applied Probability,
Vol. 25,
Issue. 02,
p.
302.
Weba, Michael
1989.
Optimized regression models for time series.
Statistics,
Vol. 20,
Issue. 1,
p.
109.
Tong, Howell
1989.
Statistical Analysis and Forecasting of Economic Structural Change.
p.
279.
Andel, Jiri
1989.
On nonlinear models for time series.
Statistics,
Vol. 20,
Issue. 4,
p.
615.
Tjøstheim, Dag
1990.
Non-linear time series and Markov chains.
Advances in Applied Probability,
Vol. 22,
Issue. 03,
p.
587.
Petruccelli, Joseph D.
1990.
A comparison of tests for setar‐type non‐linearity in time series.
Journal of Forecasting,
Vol. 9,
Issue. 1,
p.
25.
Guo, Meihui
and
Petruccelli, Joseph D.
1991.
On the null recurrence and transience of a first-order SETAR model.
Journal of Applied Probability,
Vol. 28,
Issue. 03,
p.
584.
Lim, K. S.
1992.
ON THE STABILITY OF A THRESHOLD AR(1) WITHOUT INTERCEPTS.
Journal of Time Series Analysis,
Vol. 13,
Issue. 2,
p.
119.
Liu, Jian
and
Susko, Ed
1992.
On strict stationarity and ergodicity of a non-linear ARMA model.
Journal of Applied Probability,
Vol. 29,
Issue. 02,
p.
363.
Kulkarni, P.M.
1992.
ROBUST ESTIMATION AND HYPOTHESIS TESTS FOR FIRST‐ORDER THRESHOLD AUTOREGRESSIVE MODELS.
Australian Journal of Statistics,
Vol. 34,
Issue. 1,
p.
99.
Broemeling, Lyle D.
and
Cook, Peyton
1992.
Bayesian analysis of threshold autoregressions.
Communications in Statistics - Theory and Methods,
Vol. 21,
Issue. 9,
p.
2459.
Young Hwang, Sun
and
Basawa, I.V.
1993.
Asymptotic optimal inference for a class of nonlinear time series models.
Stochastic Processes and their Applications,
Vol. 46,
Issue. 1,
p.
91.
Chen, Rong
and
Tsay, Ruey S.
1993.
Functional-Coefficient Autoregressive Models.
Journal of the American Statistical Association,
Vol. 88,
Issue. 421,
p.
298.

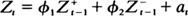 where
where 