Article contents
Super-extremal processes and the argmax process
Published online by Cambridge University Press: 14 July 2016
Abstract
In this paper, we develop the probabilistic foundations of the dynamic continuous choice problem. The underlying choice set is a compact metric space E such as the unit interval or the unit square. At each time point t, utilities for alternatives are given by a random function 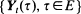 . To achieve a model of dynamic continuous choice, the theory of classical vector-valued extremal processes is extended to super-extremal processesY= {Yt, t > 0}. At any t > 0, Y t is a random upper semicontinuous function on a locally compact, separable, metric space E. General path properties of Y are discussed and it is shown that Y is Markov with state-space US(E). For each t > 0, Y t is associated.
. To achieve a model of dynamic continuous choice, the theory of classical vector-valued extremal processes is extended to super-extremal processesY= {Yt, t > 0}. At any t > 0, Y t is a random upper semicontinuous function on a locally compact, separable, metric space E. General path properties of Y are discussed and it is shown that Y is Markov with state-space US(E). For each t > 0, Y t is associated.
For a compact metric E, we consider the argmax process M = {Mt, t > 0}, where 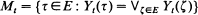 . In the dynamic continuous choice application, the argmax process M represents the evolution of the set of random utility maximizing alternatives. M is a closed set-valued random process, and its path properties are investigated.
. In the dynamic continuous choice application, the argmax process M represents the evolution of the set of random utility maximizing alternatives. M is a closed set-valued random process, and its path properties are investigated.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Applied Probability Trust 1994
Footnotes
Partially supported by NSF Grant DMS 9100027.
Partially supported by the Natural Sciences and Engineering Research Council of Canada.
References
- 3
- Cited by

