Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Embrechts, Paul
Goldie, Charles M.
and
Veraverbeke, No�l
1979.
Subexponentiality and infinite divisibility.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 49,
Issue. 3,
p.
335.
Embrechts, Paul
and
Goldie, Charles M.
1980.
On closure and factorization properties of subexponential and related distributions.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 29,
Issue. 2,
p.
243.
Maller, R. A.
1981.
Some Properties of stochastic compactness.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 30,
Issue. 3,
p.
264.
Embrechts, Paul
1983.
A property of the generalized inverse Gaussian distribution with some applications.
Journal of Applied Probability,
Vol. 20,
Issue. 03,
p.
537.
Embrechts, Paul
and
Omey, Edward
1984.
A property of longtailed distributions.
Journal of Applied Probability,
Vol. 21,
Issue. 01,
p.
80.
Pakes, Anthony G.
1988.
The Markov branching process with density-independent catastrophes I. Behaviour of extinction probabilities.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 103,
Issue. 2,
p.
351.
Klüppelberg, Claudia
1988.
Subexponential distributions and integrated tails.
Journal of Applied Probability,
Vol. 25,
Issue. 01,
p.
132.
Murphree, Emily S.
1989.
Some new results on the subexponential class.
Journal of Applied Probability,
Vol. 26,
Issue. 04,
p.
892.
Leslie, J. R.
1989.
On the non-closure under convolution of the subexponential family.
Journal of Applied Probability,
Vol. 26,
Issue. 01,
p.
58.
Bertoin, J.
and
Doney, R. A.
1994.
On the local behaviour of ladder height distributions.
Journal of Applied Probability,
Vol. 31,
Issue. 03,
p.
816.
Yakymiv, A. L.
1995.
Sufficient conditions for the subexponential property of the convolution of two distributions.
Mathematical Notes,
Vol. 58,
Issue. 5,
p.
1227.
Якымив, Арсен Любомирович
and
Yakymiv, Arsen Lubomirovich
1997.
Некоторые свойства субэкспоненциальных распределений.
Математические заметки,
Vol. 62,
Issue. 1,
p.
138.
Yakymiv, A. L.
1997.
Some properties of subexponential distributions.
Mathematical Notes,
Vol. 62,
Issue. 1,
p.
116.
Liu, Zhen
Nain, Philippe
Towsley, Don
and
Zhang, Zhi-Li
1999.
Asymptotic behavior of a multiplexer fed by a long-range dependent process.
Journal of Applied Probability,
Vol. 36,
Issue. 01,
p.
105.
Asmussen, S.
and
Kalashnikov, V.
1999.
Failure rates of regenerative systems with heavy tails.
Journal of Mathematical Sciences,
Vol. 93,
Issue. 4,
p.
486.
Sigman, Karl
1999.
Appendix: A primer on heavy-tailed distributions.
Queueing Systems,
Vol. 33,
Issue. 1-3,
p.
261.
Liu, Zhen
Nain, Philippe
Towsley, Don
and
Zhang, Zhi-Li
1999.
Asymptotic behavior of a multiplexer fed by a long-range dependent process.
Journal of Applied Probability,
Vol. 36,
Issue. 1,
p.
105.
Diaz, Francisco J.
1999.
Identifying Tail Behavior by Means of Residual Quantile Functions.
Journal of Computational and Graphical Statistics,
Vol. 8,
Issue. 3,
p.
493.
Borovkov, A. A.
2002.
On Subexponential Distributions and Asymptotics of the Distribution of the Maximum of Sequential Sums.
Siberian Mathematical Journal,
Vol. 43,
Issue. 6,
p.
995.
Tang, Qihe
and
Tsitsiashvili, Gurami
2003.
Randomly Weighted Sums of Subexponential Random Variables with Application to Ruin Theory.
Extremes,
Vol. 6,
Issue. 3,
p.
171.

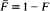 is known to imply that
is known to imply that 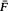 be merely of dominated variation. This note shows that
be merely of dominated variation. This note shows that 