No CrossRef data available.
Article contents
Strong convergence of peaks over a threshold
Part of:
Stochastic processes
Limit theorems
Probability theory on algebraic and topological structures
Published online by Cambridge University Press: 23 August 2023
Abstract
Extreme value theory plays an important role in providing approximation results for the extremes of a sequence of independent random variables when their distribution is unknown. An important one is given by the generalised Pareto distribution 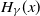 $H_\gamma(x)$ as an approximation of the distribution
$H_\gamma(x)$ as an approximation of the distribution 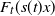 $F_t(s(t)x)$ of the excesses over a threshold t, where s(t) is a suitable norming function. We study the rate of convergence of
$F_t(s(t)x)$ of the excesses over a threshold t, where s(t) is a suitable norming function. We study the rate of convergence of 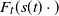 $F_t(s(t)\cdot)$ to
$F_t(s(t)\cdot)$ to 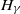 $H_\gamma$ in variational and Hellinger distances and translate it into that regarding the Kullback–Leibler divergence between the respective densities.
$H_\gamma$ in variational and Hellinger distances and translate it into that regarding the Kullback–Leibler divergence between the respective densities.
MSC classification
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust
References
Balkema, A. A. and de Haan, L. (1974). Residual life time at great age. Ann. Prob. 2, 792–804.CrossRefGoogle Scholar
Bobbia, B., Dombry, C. and Varron, D. (2021). The coupling method in extreme value theory. Bernoulli 27, 1824–1850.CrossRefGoogle Scholar
Bücher, B. and Zhou, C. (2021). A horse race between the block maxima method and the peak-over-threshold approach. Statist. Sci. 36, 360–378.CrossRefGoogle Scholar
de Haan, L. and Ferreira, A. (2006). Extreme Value Theory: An Introduction. Springer, New York.CrossRefGoogle Scholar
Dey, D. K. and Yan, J. (2016). Extreme Value Modeling and Risk Analysis: Methods and Applications. CRC Press, New York.CrossRefGoogle Scholar
Embrechts, P., Klüppelberg, C. and Mikosch, T. (2013). Modelling Extremal Events: For Insurance and Finance. Springer, Berlin.Google Scholar
Falk, M., Hüsler, J. and Reiss, R.-D. (2010). Laws of Small Numbers: Extremes and Rare Events. Birkhäuser, Basel.Google Scholar
Ghosal, S., Ghosh, J. K. and van der Vaart, A. W. (2000). Convergence rates of posterior distributions. Ann. Statist. 28, 500–531.CrossRefGoogle Scholar
Ghosal, S. and van der Vaart, A. W. (2017). Fundamentals of Nonparametric Bayesian Inference. Cambridge University Press.CrossRefGoogle Scholar
Kulik, R. and Soulier, P. (2020). Heavy-Tailed Time Series. Springer, New York.CrossRefGoogle Scholar
Pickands, III, J. (1975). Statistical inference using extreme order statistics. Ann. Statist. 3, 119–131.Google Scholar
Raoult, J.-P. and Worms, R. (2003). Rate of convergence for the generalized Pareto approximation of the excesses. Adv. Appl. Prob. 35, 1007–1027.CrossRefGoogle Scholar
Resnick, S. I. (2007). Extreme Values, Regular Variation, and Point Processes. Springer, New York.Google Scholar


