Hostname: page-component-669899f699-rg895 Total loading time: 0 Render date: 2025-04-24T20:17:26.906Z Has data issue: false hasContentIssue false
  • English
  • Français

A spatial mutation model with increasing mutation rates

Part of: Markov processes Stochastic processes

Published online by Cambridge University Press:  03 April 2023

Brian Chao Open the ORCID record for Brian Chao [Opens in a new window]  and
Jason Schweinsberg Open the ORCID record for Jason Schweinsberg [Opens in a new window]
Brian Chao*
Affiliation:
Cornell University
Jason Schweinsberg*
Affiliation:
University of California San Diego
*
*Postal address: 310 Malott Hall, Ithaca, NY 14853. Email: bc492@cornell.edu
**Postal address: Department of Mathematics, 0112; University of California, San Diego; 9500 Gilman Drive; La Jolla, CA 92093-0112. Email: jschweinsberg@ucsd.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a spatial model of cancer in which cells are points on the d-dimensional torus 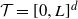$\mathcal{T}=[0,L]^d$, and each cell with 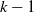$k-1$ mutations acquires a kth mutation at rate 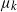$\mu_k$. We assume that the mutation rates 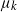$\mu_k$ are increasing, and we find the asymptotic waiting time for the first cell to acquire k mutations as the torus volume tends to infinity. This paper generalizes results on waiting for 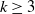$k\geq 3$ mutations in Foo et al. (2020), which considered the case in which all of the mutation rates 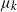$\mu_k$ are the same. In addition, we find the limiting distribution of the spatial distances between mutations for certain values of the mutation rates.

Keywords

Mutationcancerspatial population model

MSC classification

Primary: 60J99: None of the above, but in this section
Secondary: 60G55: Point processes 92D15: Problems related to evolution 92D25: Population dynamics (general)
Type
Original Article
Information
Journal of Applied Probability , Volume 60 , Issue 4 , December 2023 , pp. 1157 - 1180
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Armitage, P. and Doll, R. (1954). The age distribution of cancer and a multi-stage theory of carcinogenesis. Brit. J. Cancer 8, 1–12.CrossRefGoogle Scholar
Borodin, A., Ferrari, P. L. and Sasamoto, T. (2008). Large time asymptotics of growth models on space-like paths II: PNG and parallel TASEP. Commun. Math. Phys. 283, 417–449.CrossRefGoogle Scholar
Bramson, M. and Griffeath, D. (1980). On the Williams–Bjerknes tumour growth model II. Math. Proc. Camb. Phil. Soc. 88, 339–357.CrossRefGoogle Scholar
Bramson, M. and Griffeath, D. (1981). On the Williams–Bjerknes tumour growth model I. Ann. Prob. 9, 173–185.Google Scholar
Durrett, R., Foo, J. and Leder, K. (2016). Spatial Moran models II: Cancer initiation in spatially structured tissue. J. Math. Biol. 72, 1369–1400.CrossRefGoogle ScholarPubMed
Durrett, R. and Mayberry, J. (2011). Traveling waves of selective sweeps. Ann. Appl. Prob. 21, 699–744.CrossRefGoogle Scholar
Durrett, R. and Moseley, S. (2010). Evolution of resistance and progression to disease during clonal expansion of cancer. Theoret. Pop. Biol. 77, 42–48.Google Scholar
Durrett, R. and Moseley, S. (2015). Spatial Moran models I: Stochastic tunneling in the neutral case. Ann. Appl. Prob. 25, 104–115.CrossRefGoogle ScholarPubMed
Durrett, R., Schmidt, D. and Schweinsberg, J. (2009). A waiting time problem arising from the study of multi-stage carcinogenesis. Ann. Appl. Prob. 19, 676–718.CrossRefGoogle Scholar
Foo, J., Leder, K. and Ryser, M. D. (2014). Multifocality and recurrence risk: A quantitative model of field cancerization. J. Theoret. Biol. 355, 170–184.CrossRefGoogle Scholar
Foo, J., Leder, K. and Schweinsberg, J. (2020). Mutation timing in a spatial model of evolution. Stoch. Process. Appl. 130, 6388–6413.Google Scholar
Iwasa, Y., Michor, F., Komarova, N. L. and Nowak, M. A. (2005). Population genetics of tumor suppressor genes. J. Theoret. Biol. 233, 15–23.CrossRefGoogle ScholarPubMed
Iwasa, Y., Michor, F. and Nowak, M. A. (2004). Stochastic tunnels in evolutionary dynamics. Genetics 166, 1571–1579.CrossRefGoogle ScholarPubMed
Komarova, N. L. (2006). Spatial stochastic models for cancer initiation and progression. Bull. Math. Biol. 68, 1573–1599.CrossRefGoogle ScholarPubMed
Komarova, N. L., Sengupta, A. and Nowak, M. A. (2003). Mutation-selection networks of cancer initiation: Tumor suppressor genes and chromosomal instability. J. Theoret. Biol. 223, 433–450.CrossRefGoogle ScholarPubMed
Loeb, K. R. and Loeb, L. A. (2000). Significance of multiple mutations in cancer. Carcinogenesis 21, 379–385.CrossRefGoogle ScholarPubMed
Moolgavkar, S. H. and Luebeck, G. (1990). Two-event model for carcinogenesis: Biological, mathematical, and statistical considerations. Risk Analysis 10, 323–341.CrossRefGoogle ScholarPubMed
Moolgavkar, S. H. and Luebeck, E. G. (1992). Multistage carcinogenesis: Population-based model for colon cancer. J. Nat. Cancer Inst. 18, 610–618.CrossRefGoogle Scholar
Prähofer, M. and Spohn, H. (2000). Statistical self-similarity of one-dimensional growth processes. Physica A 279, 342–352.CrossRefGoogle Scholar
Prähofer, M. and Spohn, H. (2000). Universal distributions for growth processes in $1 + 1$ dimensions and random matrices. Phys. Rev. Lett. 84, 4882–4885.CrossRefGoogle ScholarPubMed
Prähofer, M. and Spohn, H. (2002). Scale invariance of the PNG droplet and the Airy process. J. Stat. Phys. 108, 1071–1106.Google Scholar
Prindle, M. J., Fox, E. J. and Loeb, L. A. (2010). The mutator phenotype in cancer: Molecular mechanisms and targeting strategies. Curr. Drug Targets 11, 1296–1303.CrossRefGoogle ScholarPubMed
Ryser, M. D., Lee, W. T., Ready, N. E., Leder, K. Z. and Foo, J. (2016). Quantifying the dynamics of field cancerization in tobacco-related head and neck cancer: A multiscale modeling approach. Cancer Res. 76, 7078–7088.CrossRefGoogle ScholarPubMed
Schweinsberg, J. (2008). Waiting for m mutations. Electron. J. Prob. 13, 1442–1478.CrossRefGoogle Scholar
Williams, T. and Bjerknes, R. (1972). Stochastic model for abnormal clone spread through epithelial basal layer. Nature 236, 19–21.CrossRefGoogle ScholarPubMed