Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Csenki, Attila
1991.
The joint distribution of sojourn times in finite semi-Markov processes.
Stochastic Processes and their Applications,
Vol. 39,
Issue. 2,
p.
287.
Csenki, Attila
1993.
Occupation frequencies for irreducible finite semi-markov processes with reliability applications.
Computers & Operations Research,
Vol. 20,
Issue. 3,
p.
249.
Csenki, Attila
1993.
On a counting variable in the theory of discrete-parameter Markov chains.
Statistics & Probability Letters,
Vol. 18,
Issue. 2,
p.
105.
Csenki, Attila
1993.
Sojourn times with finite time‐horizon in finite semi‐markov processes.
Applied Stochastic Models and Data Analysis,
Vol. 9,
Issue. 3,
p.
251.
Csenki, A.
1994.
On the interval reliability of systems modelled by finite semi-Markov processes.
Microelectronics Reliability,
Vol. 34,
Issue. 8,
p.
1319.
Csenki, A.
1994.
The number of working periods of a repairable Markov system during a finite time interval.
IEEE Transactions on Reliability,
Vol. 43,
Issue. 1,
p.
163.
Csenki, A.
1994.
Joint availability of systems modelled by finite semi–markov processes.
Applied Stochastic Models and Data Analysis,
Vol. 10,
Issue. 4,
p.
279.
Csenki, A.
1995.
An integral equation approach to the interval reliability of systems modelled by finite semi-Markov processes.
Reliability Engineering & System Safety,
Vol. 47,
Issue. 1,
p.
37.
Csenki, Attila
1995.
The number of visits to a subset of the state space by a discrete-parameter semi-Markov process.
Statistics & Probability Letters,
Vol. 22,
Issue. 1,
p.
71.
csenki, Attila
1995.
Mission Availability For Repairable Semi-Markov Systems: Analytical Results And Computational Implementation.
Statistics,
Vol. 26,
Issue. 1,
p.
75.
Ball, Frank
and
Davies, Sue
1997.
Clustering of Bursts of Openings in Markov and Semi-Markov Models of Single Channel Gating.
Advances in Applied Probability,
Vol. 29,
Issue. 1,
p.
92.
Smith, M.A.J.
Aven, T.
Dekker, R.
and
Van der Duyn Schouten, F.A.
1997.
Advances in Safety and Reliability.
p.
1727.
Ball, Frank
1999.
Central limit theorems for multivariate semi-Markov sequences and processes, with applications.
Journal of Applied Probability,
Vol. 36,
Issue. 02,
p.
415.
Ball, Frank
1999.
Central limit theorems for multivariate semi-Markov sequences and processes, with applications.
Journal of Applied Probability,
Vol. 36,
Issue. 2,
p.
415.
Csenki, Attila
2002.
Stochastic Models in Reliability and Maintenance.
p.
219.
Ball, Frank
and
Milne, Robin K.
2005.
Simple derivations of properties of counting processes associated with Markov renewal processes.
Journal of Applied Probability,
Vol. 42,
Issue. 04,
p.
1031.

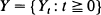 is considered whose finite state space is partitioned into two non-empty sets
is considered whose finite state space is partitioned into two non-empty sets 