Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Boland, Philip J.
Hu, Taizhong
Shaked, Moshe
and
Shanthikumar, J. George
2002.
Modeling Uncertainty.
Vol. 46,
Issue. ,
p.
607.
Lihong, Sun
and
Xinsheng, Zhang
2005.
Stochastic comparisons of order statistics from gamma distributions.
Journal of Multivariate Analysis,
Vol. 93,
Issue. 1,
p.
112.
Bon, Jean-Louis
and
Păltănea, Eugen
2006.
Comparison of order statistics in a random sequence to the same statistics with i.i.d. variables.
ESAIM: Probability and Statistics,
Vol. 10,
Issue. ,
p.
1.
Khaledi, Baha-Eldin
and
Kochar, Subhash
2006.
Weibull distribution: Some stochastic comparisons results.
Journal of Statistical Planning and Inference,
Vol. 136,
Issue. 9,
p.
3121.
Jeon, Jongwoo
Kochar, Subhash
and
Park, Chul Gyu
2006.
Dispersive ordering—Some applications and examples.
Statistical Papers,
Vol. 47,
Issue. 2,
p.
227.
Kochar, Subhash
and
Xu, Maochao
2007.
STOCHASTIC COMPARISONS OF PARALLEL SYSTEMS WHEN COMPONENTS HAVE PROPORTIONAL HAZARD RATES.
Probability in the Engineering and Informational Sciences,
Vol. 21,
Issue. 4,
p.
597.
Navarro, Jorge
2007.
Tail hazard rate ordering properties of order statistics and coherent systems.
Naval Research Logistics (NRL),
Vol. 54,
Issue. 8,
p.
820.
Khaledi, Baha-Eldin
and
Kochar, Subhash
2007.
Stochastic Orderings of Order Statistics of Independent Random Variables with Different Scale Parameters.
Communications in Statistics - Theory and Methods,
Vol. 36,
Issue. 7,
p.
1441.
Păltănea, Eugen
2008.
On the comparison in hazard rate ordering of fail-safe systems.
Journal of Statistical Planning and Inference,
Vol. 138,
Issue. 7,
p.
1993.
Zhao, Peng
Li, Xiaohu
and
Balakrishnan, N.
2009.
Likelihood ratio order of the second order statistic from independent heterogeneous exponential random variables.
Journal of Multivariate Analysis,
Vol. 100,
Issue. 5,
p.
952.
Zhao, Peng
and
Balakrishnan, N.
2009.
Characterization of MRL order of fail-safe systems with heterogeneous exponential components.
Journal of Statistical Planning and Inference,
Vol. 139,
Issue. 9,
p.
3027.
Genest, Christian
Kochar, Subhash C.
and
Xu, Maochao
2009.
On the range of heterogeneous samples.
Journal of Multivariate Analysis,
Vol. 100,
Issue. 8,
p.
1587.
Kochar, Subhash
and
Xu, Maochao
2009.
Comparisons of Parallel Systems According to the Convex Transform Order.
Journal of Applied Probability,
Vol. 46,
Issue. 02,
p.
342.
Da, Gaofeng
Ding, Weiyong
and
Li, Xiaohu
2010.
On hazard rate ordering of parallel systems with two independent components.
Journal of Statistical Planning and Inference,
Vol. 140,
Issue. 7,
p.
2148.
Mao, Tiantian
and
Hu, Taizhong
2010.
EQUIVALENT CHARACTERIZATIONS ON ORDERINGS OF ORDER STATISTICS AND SAMPLE RANGES.
Probability in the Engineering and Informational Sciences,
Vol. 24,
Issue. 2,
p.
245.
Joo, Sui
and
Mi, Jie
2010.
Some properties of hazard rate functions of systems with two components.
Journal of Statistical Planning and Inference,
Vol. 140,
Issue. 2,
p.
444.
Păltănea, Eugen
2011.
Bounds for mixtures of order statistics from exponentials and applications.
Journal of Multivariate Analysis,
Vol. 102,
Issue. 5,
p.
896.
Khaledi, Baha-Eldin
Farsinezhad, Sepideh
and
Kochar, Subhash C.
2011.
Stochastic comparisons of order statistics in the scale model.
Journal of Statistical Planning and Inference,
Vol. 141,
Issue. 1,
p.
276.
Zhao, Peng
2011.
ON PARALLEL SYSTEMS WITH HETEROGENEOUS GAMMA COMPONENTS.
Probability in the Engineering and Informational Sciences,
Vol. 25,
Issue. 3,
p.
369.
Zhao, Bing
Li, Dongmei
and
Ma, Mingjian
2011.
Stochastic Comparisons for k-out-of-N(F) System of Random Numbers of Units.
Journal of Computers,
Vol. 6,
Issue. 11,
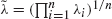 . Let Y 1,…,Y n be a random sample of size n from an exponential distribution with common hazard rate ̃λ = (∏i=1 n λi )1/n , the geometric mean of the λis. Let X n:n = max{X 1,…,X n }. It is shown that X n:n is greater than Y n:n according to dispersive as well as hazard rate orderings. These results lead to a lower bound for the variance of X n:n and an upper bound on the hazard rate function of X n:n in terms of
. Let Y 1,…,Y n be a random sample of size n from an exponential distribution with common hazard rate ̃λ = (∏i=1 n λi )1/n , the geometric mean of the λis. Let X n:n = max{X 1,…,X n }. It is shown that X n:n is greater than Y n:n according to dispersive as well as hazard rate orderings. These results lead to a lower bound for the variance of X n:n and an upper bound on the hazard rate function of X n:n in terms of 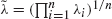 . These bounds are sharper than those obtained by Dykstra et al. ((1997), J. Statist. Plann. Inference65, 203–211), which are in terms of the arithmetic mean of the λi s. Furthermore, let X 1 *,…,X n ∗ be another set of independent exponential random variables with X i ∗ having hazard rate λi ∗, i = 1,…,n. It is proved that if (logλ1,…,logλn ) weakly majorizes (logλ1 ∗,…,logλn ∗, then X n:n is stochastically greater than X n:n ∗.
. These bounds are sharper than those obtained by Dykstra et al. ((1997), J. Statist. Plann. Inference65, 203–211), which are in terms of the arithmetic mean of the λi s. Furthermore, let X 1 *,…,X n ∗ be another set of independent exponential random variables with X i ∗ having hazard rate λi ∗, i = 1,…,n. It is proved that if (logλ1,…,logλn ) weakly majorizes (logλ1 ∗,…,logλn ∗, then X n:n is stochastically greater than X n:n ∗.