Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sheu, Shey-Huei
1990.
Periodic replacement when minimal repair costs depend on the age and the number of minimal repairs for a multi-unit system.
Microelectronics Reliability,
Vol. 30,
Issue. 4,
p.
713.
He, Shengwu
and
Wang, Jiagang
1990.
Thinning of Point Processes—Martingale Method.
Probability in the Engineering and Informational Sciences,
Vol. 4,
Issue. 1,
p.
117.
Sheu, Shey-Huei
1990.
Periodic replacement when minimal repair costs depend on the age and the number of minimal repair for a multi-unit system.
Microelectronics Reliability,
Vol. 30,
Issue. 3,
p.
565.
Sheu, Shey-Huei
1991.
A general age replacement model with minimal repair and general random repair cost.
Microelectronics Reliability,
Vol. 31,
Issue. 5,
p.
1009.
Sheu, Shey-Huei
1992.
A general replacement of a system subject to shocks.
Microelectronics Reliability,
Vol. 32,
Issue. 5,
p.
657.
Sheu, Shey-Huei
1992.
Optimal block replacement policies with multiple choice at failure.
Journal of Applied Probability,
Vol. 29,
Issue. 01,
p.
129.
Sheu, Shey-Huei
and
Liou, Ching-Tien
1992.
An ordering policy with age-dependent minimal repair and age-dependent random repair costs.
Microelectronics Reliability,
Vol. 32,
Issue. 8,
p.
1105.
Sheu, Shey-Huei
and
Liou, Ching-Tien
1992.
Optimal replacement of a k-out-of-n system subject to shocks.
Microelectronics Reliability,
Vol. 32,
Issue. 5,
p.
649.
Sheu, Shey-Huei
and
Liou, Ching-Tien
1992.
An age replacement policy with minimal repair and general random repair cost.
Microelectronics Reliability,
Vol. 32,
Issue. 9,
p.
1283.
Chen, C.S.
and
Savits, T.H.
1993.
Some remarks on compound nonhomogeneous Poisson processes.
Statistics & Probability Letters,
Vol. 17,
Issue. 3,
p.
179.
SHEU, SHEY-HUEI
1993.
Optimal testing policy for a computer system with fault margin.
International Journal of Systems Science,
Vol. 24,
Issue. 8,
p.
1611.
SHEU, SHEY-HUEI
and
LIOU, CHING-TIEN
1993.
Optimum ordering policies with age-dependent minimal repair and two types of lead times.
International Journal of Systems Science,
Vol. 24,
Issue. 2,
p.
253.
Sheu, Shey-Huei
1993.
A generalized model for determining optimal number of minimal repairs before replacement.
European Journal of Operational Research,
Vol. 69,
Issue. 1,
p.
38.
Sheu, Shey-Huei
1994.
Extended block replacement policy with used item and general random minimal repair cost.
European Journal of Operational Research,
Vol. 79,
Issue. 3,
p.
405.
Sheu, Shey-Huei
and
Kuo, Chung-Ming
1994.
Optimization problems in systems with minimal repair.
Reliability Engineering & System Safety,
Vol. 44,
Issue. 1,
p.
77.
Shey-Huei Sheu
Griffith, William S.
and
Toshio Nakagawa
1995.
Extended optimal replacement model with random minimal repair costs.
European Journal of Operational Research,
Vol. 85,
Issue. 3,
p.
636.
SHEU, SHEY-HUEI
and
LIOU, CHING-TIEN
1995.
A generalized sequential preventive maintenance policy for repairable systems with general random minimal repair costs.
International Journal of Systems Science,
Vol. 26,
Issue. 3,
p.
681.
SHEU, SHEY-HUEI
1996.
Optimum age replacement of a system subject to shocks with random lead time.
International Journal of Systems Science,
Vol. 27,
Issue. 12,
p.
1417.
SHEU, SHEY-HUEI
1997.
A generalized model for jointly determining the optimal ordering point and the optimal number of minimal repairs before replacement.
International Journal of Systems Science,
Vol. 28,
Issue. 8,
p.
759.
Sheu, Shey-Huei
and
Jhang, Jhy-Ping
1997.
A generalized group maintenance policy.
European Journal of Operational Research,
Vol. 96,
Issue. 2,
p.
232.

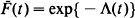 .
.