Article contents
Some characterizations of exponential or geometric distributions in a non-stationary record value model
Published online by Cambridge University Press: 14 July 2016
Abstract
Let {Fn }n ≧ 0 be a sequence of c.d.f. and let {Rn }n ≧ 1 be the sequence of record values in a non-stationary record model where after the (n − 1)th record the population is distributed according to Fn. Then the equidistribution of the nth population and the record increment Rn – Rn – 1 (i.e. Rn – Rn – 1~ Fn ) characterizes Fn to have an exponentially decreasing hazard function. To be more precise Fn is the exponential distribution if the support of Rn – 1 generates a dense subgroup in 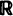 and otherwise the entity of all possible solutions can be obtained in the following way: let for simplicity the above additive subgroup be
and otherwise the entity of all possible solutions can be obtained in the following way: let for simplicity the above additive subgroup be 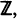 any c.d.f. F satisfying F(0) = 0, F(1) < 1 can be chosen arbitrarily. Setting λ = – log(1 – F(1)), Fn (x) = 1 – F(x – [x])exp(–λ [x])
any c.d.f. F satisfying F(0) = 0, F(1) < 1 can be chosen arbitrarily. Setting λ = – log(1 – F(1)), Fn (x) = 1 – F(x – [x])exp(–λ [x]) 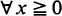 is an admissible solution coinciding with F on the interval [0, 1] ([x] denotes the integer part of x). Simple additional assumptions ensuring that Fn is either exponential or geometric are given. Similar results for exponential or geometric tail distributions based on the independence of Rn – 1 and Rn – Rn – 1 are proved.
is an admissible solution coinciding with F on the interval [0, 1] ([x] denotes the integer part of x). Simple additional assumptions ensuring that Fn is either exponential or geometric are given. Similar results for exponential or geometric tail distributions based on the independence of Rn – 1 and Rn – Rn – 1 are proved.
Keywords
MSC classification
Information
- Type
- Research Papers
- Information
- Copyright
- Copyright © Applied Probability Trust 1993
References
- 1
- Cited by

